working with k-NN, we all know that the k-NN strategy may be very naive. It retains your complete coaching dataset in reminiscence, depends on uncooked distances, and doesn’t be taught any construction from the information.
We already started to enhance the k-NN classifier, and in right now’s article, we are going to implement these totally different fashions:
- GNB: Gaussian Naive Bayes
- LDA: Linear Discriminant Evaluation
- QDA: Quadratic Discriminant Evaluation
For all these fashions, the distribution is taken into account as Gaussian. So on the finish, we may even see an strategy to get a extra custom-made distribution.
Should you learn my earlier article, listed below are some questions for you:
- What’s the relationship between LDA and QDA?
- What’s the relation between GBN and QDA?
- What occurs if the information just isn’t Gaussian in any respect?
- What’s the methodology to get a custom-made distribution?
- What’s linear in LDA? What’s quadratic in QDA?
When studying by way of the article, you should use this Excel/Google sheet.
Nearest Centroids: What This Mannequin Actually Is
Let’s do a fast recap about what we already started yesterday.
We launched a easy thought: after we calculate the common of every steady characteristic inside a category, that class collapses into one single consultant level.
This provides us the Nearest Centroids mannequin.
Every class is summarized by its centroid, the common of all its characteristic values.
Now, allow us to take into consideration this from a Machine Studying viewpoint.
We often separate the method into two components: the coaching step and the hyperparameter tuning step.
For Nearest Centroids, we are able to draw a small “mannequin card” to grasp what this mannequin actually is:
- How is the mannequin educated? By computing one common vector per class. Nothing extra.
- Does it deal with lacking values? Sure. A centroid may be computed utilizing all accessible (non-empty) values.
- Does scale matter? Sure, completely, as a result of distance to a centroid is determined by the items of every characteristic.
- What are the hyperparameters? None.
We mentioned that the k-NN classifier is probably not an actual machine studying mannequin as a result of it’s not an precise mannequin.
For Nearest Centroids, we are able to say that it’s not actually a machine studying mannequin as a result of it can’t be tuned. So what about overfitting and underfitting?
Properly, the mannequin is so easy that it can not memorize noise in the identical method k-NN does.
So, Nearest Centroids will solely are inclined to underfit when courses are advanced or not properly separated, as a result of one single centroid can not seize their full construction.
Understanding Class Form with One Characteristic: Including Variance
Now, on this part, we are going to use just one steady characteristic, and a pair of courses.
Thus far, we used just one statistic per class: the common worth.
Allow us to now add a second piece of data: the variance (or equivalently, the usual deviation).
This tells us how “unfold out” every class is round its common.
A pure query seems instantly: Which variance ought to we use?
Probably the most intuitive reply is to compute one variance per class, as a result of every class might need a special unfold.
However there may be one other risk: we may compute one widespread variance for each courses, often as a weighted common of the category variances.
This feels a bit unnatural at first, however we are going to see later that this concept leads on to LDA.
So the desk under offers us every part we’d like for this mannequin, in reality, for each variations (LDA and QDA) of the mannequin.
- the variety of observations in every class (to weight the courses)
- the imply of every class
- the usual deviation of every class
- and the widespread commonplace deviation throughout each courses
With these values, your complete mannequin is totally outlined.

Now, as soon as we’ve a typical deviation, we are able to construct a extra refined distance: the gap to the centroid divided by the usual deviation.
Why will we do that?
As a result of this provides a distance that’s scaled by how variable the category is.
If a category has a big commonplace deviation, being removed from its centroid isn’t a surprise.
If a category has a really small commonplace deviation, even a small deviation turns into vital.
This easy normalization turns our Euclidean distance into one thing a bit bit extra significant, that represents the form of every class.
This distance was launched by Mahalanobis, so we name it the Mahalanobis distance.
Now we are able to do all these calculations instantly within the Excel file.

The formulation are easy, and with conditional formatting, we are able to clearly see how the gap to every heart adjustments and the way the scaling impacts the outcomes.

Now, let’s do some plots, all the time in Excel.
This diagram under reveals the total development: how we begin from the Mahalanobis distance, transfer to the probability underneath every class distribution, and eventually receive the chance prediction.

LDA vs. QDA, what will we see?
With only one characteristic, the distinction turns into very simple to visualise.
For LDA, the separation on the x-axis is all the time lower into two components. That is why the strategy is named Linear Discriminant Evaluation.
For QDA, even with just one characteristic, the mannequin produces two lower factors on the x-axis. In greater dimensions, this turns into a curved boundary, described by a quadratic operate. Therefore, the title Quadratic Discriminant Evaluation.

And you’ll instantly modify the parameters to see how they influence the choice boundary.
The adjustments within the means or variances will change the frontier, and Excel makes these results very simple to visualise.
By the best way, does the form of the LDA chance curve remind you of a mannequin that you just absolutely know? Sure, it appears precisely the identical.
You’ll be able to already guess which one, proper?
However now the true query is: are they actually the identical mannequin? And if not, how do they differ?

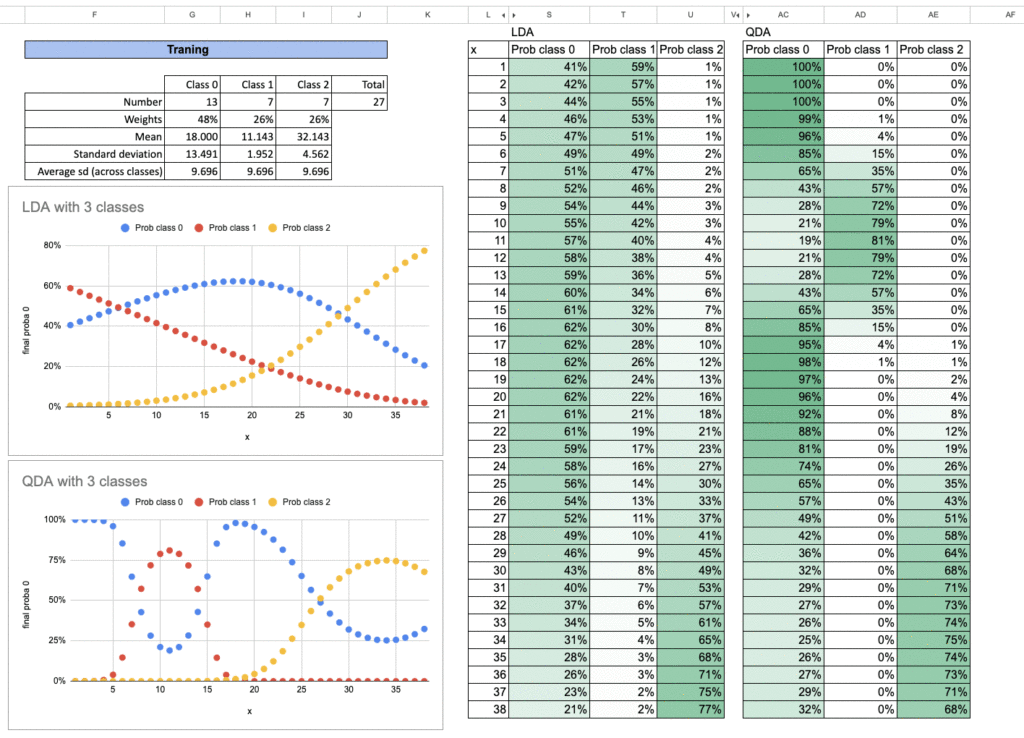
We are able to additionally research the case with three courses. You’ll be able to do this your self as an train in Excel.
Listed below are the outcomes. For every class, we repeat precisely the identical process. And for the ultimate chance prediction, we merely sum all of the likelihoods and take the proportion of every one.

Once more, this strategy can be utilized in one other well-known mannequin.
Are you aware which one? It’s way more acquainted to most individuals, and this reveals how intently linked these fashions actually are.
Once you perceive one among them, you robotically perceive the others a lot better.
Class Form in 2D: Variance Solely or Covariance as Properly?
With one characteristic, we don’t speak about dependency, as there may be none. So on this case, QDA behaves precisely like Gaussian Naive Bayes. As a result of we often enable every class to have its personal variance, which is completely pure.
The distinction will seem after we transfer to 2 or extra options. At that time, we are going to distinguish instances of how the mannequin treats the covariance between the options.
Gaussian Naive Bayes makes one very sturdy simplifying assumption:
the options are unbiased. That is the rationale for the phrase Naive in its title.
LDA and QDA, nonetheless, don’t make this assumption. They permit interactions between options, and that is what generates linear or quadratic boundaries in greater dimensions.
Let’s do the exercice in Excel!
Gaussian Naive Bayes: no covariance
Allow us to start with the best case: Gaussian Naive Bayes.
So, we don’t have to compute any covariance in any respect, as a result of the mannequin assumes that the options are unbiased.
For instance this, we are able to take a look at a small instance with three courses.

QDA: every class has its personal covariance
For QDA, we now must calculate the covariance matrix for every class.
And as soon as we’ve it, we additionally have to compute its inverse, as a result of it’s used instantly within the components for the gap and the probability.
So there are just a few extra parameters to compute in comparison with Gaussian Naive Bayes.

LDA: all courses share the identical covariance
For LDA, all courses share the identical covariance matrix, which reduces the variety of parameters and forces the choice boundary to be linear.
Despite the fact that the mannequin is less complicated, it stays very efficient in lots of conditions, particularly when the quantity of knowledge is restricted.

Custom-made Class Distributions: Past the Gaussian Assumption
Thus far, we solely talked about Gaussian distributions. And it’s for its simplificity. And we can also use different distributions. So even in Excel, it is rather simple to alter.
In actuality, knowledge often don’t comply with an ideal Gaussian curve.
For exploring a dataset, we use the empiric density plots virtually each time. They provide a direct visible feeling of how the information is distributed.
And the kernel density estimator (KDE) as a non-parametric methodology, is commonly used.
BUT, in observe, KDE isn’t used as a full classification mannequin. It isn’t very handy, and its predictions are sometimes delicate to the selection of bandwidth.
And what’s fascinating is that this concept of kernels will come again once more after we focus on different fashions.
So regardless that we present it right here primarily for exploration, it’s an important constructing block in machine studying.

Conclusion
In the present day, we adopted a pure path that begins with easy averages and regularly results in full probabilistic fashions.
- Nearest Centroids compresses every class into one level.
- Gaussian Naive Bayes provides the notion of variance, and assumes the independance of the options.
- QDA offers every class its personal variance or covariance
- LDA simplifies the form by sharing the covariance.
We even noticed that we are able to step outdoors the Gaussian world and discover custom-made distributions.
All these fashions are linked by the identical thought: a brand new statement belongs to the category it most resembles.
The distinction is how we outline resemblance, by distance, by variance, by covariance, or by a full chance distribution.
For all these fashions, we are able to do the 2 steps simply in Excel:
- step one is to estimate the paramters, which may be thought of because the mannequin coaching
- the inference step that’s to calculate the gap and the chance for every class

Yet one more factor
Earlier than closing this text, allow us to draw a small cartography of distance-based supervised fashions.
We now have two important households:
- native distance fashions
- international distance fashions
For native distance, we already know the 2 classical ones:
- k-NN regressor
- k-NN classifier
Each predict by neighbors and utilizing the native geometry of the information.
For international distance, all of the fashions we studied right now belong to the classification world.
Why?
As a result of international distance requires facilities outlined by courses.
We measure how shut a brand new statement is to every class prototype?
However what about regression?
It appears that evidently this notion of worldwide distance doesn’t exist for regression, or does it actually?
The reply is sure, it does exist…