we’re.
That is the mannequin that motivated me, from the very starting, to make use of Excel to raised perceive Machine Studying.
And right now, you will see a completely different clarification of SVM than you often see, which is the one with:
- margin separators,
- distances to a hyperplane,
- geometric constructions first.
As an alternative, we are going to construct the mannequin step-by-step, ranging from issues we already know.
So perhaps that is additionally the day you lastly say “oh, I perceive higher now.”
Constructing a New Mannequin on What We already Know
One in every of my essential studying ideas is easy:
at all times begin from what we already know.
Earlier than SVM, we already studied:
- logistic regression,
- penalization and regularization.
We are going to use these fashions and ideas right now.
The concept is to not introduce a brand new mannequin, however to rework an present one.
Coaching datasets and label conference
We use two datasets that I generated for example the 2 attainable conditions a linear classifier can face:
- one dataset is fully separable
- the opposite is not fully separable
It’s possible you’ll already know why we use these two datasets, whereas we solely use one, proper?
We additionally use the label conference -1 and 1 as a substitute of 0 and 1.
In logistic regression, earlier than making use of the sigmoid, we compute a logit. And we will name it f, this can be a linear rating.
This amount is a linear rating that may take any actual worth, from −∞ to +∞.
- constructive values correspond to at least one class,
- adverse values correspond to the opposite,
- zero is the choice boundary.
Utilizing labels -1 and 1 matches this interpretation naturally.
It emphasizes the signal of the logit, with out going by way of possibilities.
So, we’re working with a pure linear mannequin, not inside the GLM framework.
There is no such thing as a sigmoid, no likelihood, solely a linear resolution rating.
A compact strategy to specific this concept is to have a look at the amount:
y(ax + b) = y f(x)
- If this worth is constructive, the purpose is appropriately categorised.
- Whether it is massive, the classification is assured.
- Whether it is adverse, the purpose is misclassified.
At this level, we’re nonetheless not speaking about SVMs.
We’re solely making specific what good classification means in a linear setting.
From log-loss to a brand new loss perform
With this conference, we will write the log-loss for logistic regression immediately as a perform of the amount:
y f(x) = y (ax+b)
We will plot this loss as a perform of yf(x).
Now, allow us to introduce a brand new loss perform known as the hinge loss.
Once we plot the 2 losses on the identical graph, we will see that they’re fairly related in form.
Do you keep in mind Gini vs. Entropy in Determination Tree Classifiers?
The comparability may be very related right here.

In each circumstances, the thought is to penalize:
- factors which might be misclassified yf(x)<0,
- factors which might be too near the choice boundary.
The distinction is in how this penalty is utilized.
- The log-loss penalizes errors in a clean and progressive means.
Even well-classified factors are nonetheless barely penalized. - The hinge loss is extra direct and abrupt.
As soon as some extent is appropriately categorised with a ample margin, it’s not penalized in any respect.
So the purpose is to not change what we contemplate an excellent or unhealthy classification,
however to simplify the way in which we penalize it.
One query naturally follows.
Might we additionally use a squared loss?
In any case, linear regression will also be used as a classifier.
However once we do that, we instantly see the issue:
the squared loss retains penalizing factors which might be already very properly categorised.
As an alternative of specializing in the choice boundary, the mannequin tries to suit actual numeric targets.
Because of this linear regression is often a poor classifier, and why the selection of the loss perform issues a lot.

Description of the brand new mannequin
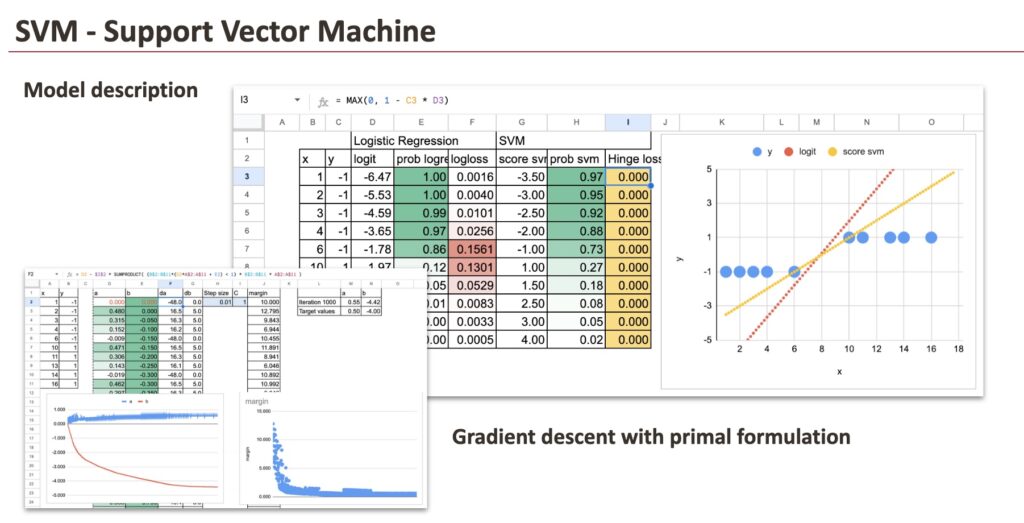
Allow us to now assume that the mannequin is already educated and look immediately on the outcomes.
For each fashions, we compute precisely the identical portions:
- the linear rating (and it’s known as logit for Logistic Regression)
- the likelihood (we will simply apply the sigmoid perform in each circumstances),
- and the loss worth.
This permits a direct, point-by-point comparability between the 2 approaches.
Though the loss capabilities are completely different, the linear scores and the ensuing classifications are very related on this dataset.
For the fully separable dataset, the result’s speedy: all factors are appropriately categorised and lie sufficiently removed from the choice boundary. As a consequence, the hinge loss is the same as zero for each commentary.
This results in an necessary conclusion.
When the information is completely separable, there’s not a singular resolution. In actual fact, there are infinitely many linear resolution capabilities that obtain precisely the identical end result. We will shift the road, rotate it barely, or rescale the coefficients, and the classification stays good, with zero loss all over the place.
So what will we do subsequent?
We introduce regularization.
Simply as in ridge regression, we add a penalty on the dimension of the coefficients. This extra time period doesn’t enhance classification accuracy, but it surely permits us to pick one resolution amongst all of the attainable ones.
So in our dataset, we get the one with the smallest slope a.

And congratulations, we’ve simply constructed the SVM mannequin.
We will now simply write down the price perform of the 2 fashions: Logistic Regression and SVM.
Do you keep in mind that Logistic Regression could be regularized, and it’s nonetheless known as so, proper?

Now, why does the mannequin embrace the time period “Help Vectors”?
In the event you take a look at the dataset, you’ll be able to see that just a few factors, for instance those with values 6 and 10, are sufficient to find out the choice boundary. These factors are known as assist vectors.
At this stage, with the attitude we’re utilizing, we can not establish them immediately.
We are going to see later that one other viewpoint makes them seem naturally.
And we will do the identical train for an additional dataset, with non-separable dataset, however the precept is identical. Nothing modified.
However now, we will see that for certains factors, the hinge loss is just not zero. In our case under, we will see visually that there are 4 factors that we want as Help Vectors.

SVM Mannequin Coaching with Gradient Descent
We now practice the SVM mannequin explicitly, utilizing gradient descent.
Nothing new is launched right here. We reuse the identical optimization logic we already utilized to linear and logistic regression.
New conference: Lambda (λ) or C
In lots of fashions we studied beforehand, akin to ridge or logistic regression, the target perform is written as:
data-fit loss +λ ∥w∥
Right here, the regularization parameter λ controls the penalty on the dimensions of the coefficients.
For SVMs, the same old conference is barely completely different. We somewhat use C in entrance of the data-fit time period.

Each formulations are equal.
They solely differ by a rescaling of the target perform.
We hold the parameter C as a result of it’s the usual notation utilized in SVMs. And we are going to see why we’ve this conference later.
Gradient (subgradient)
We work with a linear resolution perform, and we will outline the margin for every level as: mi = yi (axi + b)
Solely observations such that mi<1 contribute to the hinge loss.
The subgradients of the target are as follows, and we will implement in Excel, utilizing logical masks and SUMPRODUCT.

Parameter replace
With a studying price or step dimension η, the gradient descent updates are as follows, and we will do the same old method:

We iterate these updates till convergence.
And, by the way in which, this coaching process additionally provides us one thing very good to visualise. At every iteration, because the coefficients are up to date, the dimension of the margin modifications.
So we will visualize, step-by-step, how the margin evolves in the course of the studying course of.
Optimization vs. geometric formulation of SVM
This determine under reveals the similar goal perform of the SVM mannequin written in two completely different languages.

On the left, the mannequin is expressed as an optimization drawback.
We decrease a mixture of two issues:
- a time period that retains the mannequin easy, by penalizing massive coefficients,
- and a time period that penalizes classification errors or margin violations.
That is the view we’ve been utilizing to this point. It’s pure once we suppose when it comes to loss capabilities, regularization, and gradient descent. It’s the most handy kind for implementation and optimization.
On the precise, the identical mannequin is expressed in a geometric means.
As an alternative of speaking about losses, we speak about:
- margins,
- constraints,
- and distances to the separating boundary.
When the information is completely separable, the mannequin appears to be like for the separating line with the largest attainable margin, with out permitting any violation. That is the hard-margin case.
When good separation is unimaginable, violations are allowed, however they’re penalized. This results in the soft-margin case.
What’s necessary to know is that these two views are strictly equal.
The optimization formulation robotically enforces the geometric constraints:
- penalizing massive coefficients corresponds to maximizing the margin,
- penalizing hinge violations corresponds to permitting, however controlling, margin violations.
So this isn’t two completely different fashions, and never two completely different concepts.
It’s the similar SVM, seen from two complementary views.
As soon as this equivalence is evident, the SVM turns into a lot much less mysterious: it’s merely a linear mannequin with a specific means of measuring errors and controlling complexity, which naturally results in the maximum-margin interpretation everybody is aware of.
Unified Linear Classifier
From the optimization viewpoint, we will now take a step again and take a look at the larger image.
What we’ve constructed isn’t just “the SVM”, however a common linear classification framework.
A linear classifier is outlined by three impartial decisions:
- a linear resolution perform,
- a loss perform,
- a regularization time period.
As soon as that is clear, many fashions seem as easy mixtures of those components.
In follow, that is precisely what we will do with SGDClassifier in scikit-learn.

From the identical viewpoint, we will:
- mix the hinge loss with L1 regularization,
- exchange hinge loss with squared hinge loss,
- use log-loss, hinge loss, or different margin-based losses,
- select L2 or L1 penalties relying on the specified conduct.
Every alternative modifications how errors are penalized or how coefficients are managed, however the underlying mannequin stays the identical: a linear resolution perform educated by optimization.
Primal vs Twin Formulation
It’s possible you’ll have already got heard concerning the twin kind of SVM.
Thus far, we’ve labored solely within the primal kind:
- we optimized the mannequin coefficients immediately,
- utilizing loss capabilities and regularization.
The twin kind is one other strategy to write the identical optimization drawback.
As an alternative of assigning weights to options, the twin kind assigns a coefficient, often known as alpha, to every knowledge level.
We is not going to derive or implement the twin kind in Excel, however we will nonetheless observe its end result.
Utilizing scikit-learn, we will compute the alpha values and confirm that:
- the primal and twin kinds result in the similar mannequin,
- similar resolution boundary, similar predictions.

What makes the twin kind significantly attention-grabbing for SVM is that:
- most alpha values are precisely zero,
- just a few knowledge factors have non-zero alpha.
These factors are the assist vectors.
This conduct is restricted to margin-based losses just like the hinge loss.
Lastly, the twin kind additionally explains why SVMs can use the kernel trick.
By working with similarities between knowledge factors, we will construct non-linear classifiers with out altering the optimization framework.
We are going to see this tomorrow.
Conclusion
On this article, we didn’t strategy SVM as a geometrical object with sophisticated formulation. As an alternative, we constructed it step-by-step, ranging from fashions we already know.
By altering solely the loss perform, then including regularization, we naturally arrived on the SVM. The mannequin didn’t change. Solely the way in which we penalize errors did.
Seen this fashion, SVM is just not a brand new household of fashions. It’s a pure extension of linear and logistic regression, seen by way of a special loss.
We additionally confirmed that:
- the optimization view and the geometric view are equal,
- the maximum-margin interpretation comes immediately from regularization,
- and the notion of assist vectors emerges naturally from the twin perspective.
As soon as these hyperlinks are clear, SVM turns into a lot simpler to know and to position amongst different linear classifiers.
Within the subsequent step, we are going to use this new perspective to go additional, and see how kernels prolong this concept past linear fashions.