Regression, lastly!
For Day 11, I waited many days to current this mannequin. It marks the start of a new journey on this “Advent Calendar“.
Till now, we principally checked out fashions based mostly on distances, neighbors, or native density. As you might know, for tabular knowledge, resolution timber, particularly ensembles of resolution timber, are very performant.
However beginning immediately, we change to a different standpoint: the weighted method.
Linear Regression is our first step into this world.
It appears to be like easy, however it introduces the core components of recent ML: loss features, gradients, optimization, scaling, collinearity, and interpretation of coefficients.
Now, once I say, Linear Regression, I imply Extraordinary Least Sq. Linear Regression. As we progress by this “Advent Calendar” and discover associated fashions, you will notice why you will need to specify this, as a result of the title “linear regression” could be complicated.
Some individuals say that Linear Regression is not machine studying.
Their argument is that machine studying is a “new” discipline, whereas Linear Regression existed lengthy earlier than, so it can’t be thought-about ML.
That is deceptive.
Linear Regression matches completely inside machine studying as a result of:
- it learns parameters from knowledge,
- it minimizes a loss perform,
- it makes predictions on new knowledge.
In different phrases, Linear Regression is likely one of the oldest fashions, but in addition one of many most elementary in machine studying.
That is the method utilized in:
- Linear Regression,
- Logistic Regression,
- and, later, Neural Networks and LLMs.
For deep studying, this weighted, gradient-based method is the one that’s used in all places.
And in fashionable LLMs, we’re now not speaking about a number of parameters. We’re speaking about billions of weights.
On this article, our Linear Regression mannequin has precisely 2 weights.
A slope and an intercept.
That’s all.
However we’ve got to start someplace, proper?
And listed below are a number of questions you’ll be able to bear in mind as we progress by this text, and within the ones to return.
- We’ll attempt to interpret the mannequin. With one characteristic, y=ax+b, everybody is aware of {that a} is the slope and b is the intercept. However how can we interpret the coefficients the place there are 10, 100 or extra options?
- Why is collinearity between options such an issue for linear regression? And the way can we do to unravel this subject?
- Is scaling vital for linear regression?
- Can Linear regression be overfitted?
- And the way are the opposite fashions of this weighted familly (Logistic Regression, SVM, Neural Networks, Ridge, Lasso, and so forth.), all linked to the identical underlying concepts?
These questions type the thread of this text and can naturally lead us towards future subjects within the “Creation Calendar”.
Understanding the Development line in Excel
Beginning with a Easy Dataset
Allow us to start with a quite simple dataset that I generated with one characteristic.
Within the graph beneath, you’ll be able to see the characteristic variable x on the horizontal axis and the goal variable y on the vertical axis.
The purpose of Linear Regression is to seek out two numbers, a and b, such that we will write the connection:
y=a x +b
As soon as we all know a and b, this equation turns into our mannequin.
Creating the Development Line in Excel
In Google Sheets or Excel, you’ll be able to merely add a pattern line to visualise the perfect linear match.
That already provides you the results of Linear Regression.

However the function of this text is to compute these coefficients ourselves.
If we need to use the mannequin to make predictions, we have to implement it instantly.

Introducing Weights and the Value Operate
A Be aware on Weight-Primarily based Fashions
That is the primary time within the Creation Calendar that we introduce weights.
Fashions that be taught weights are sometimes referred to as parametric discriminant fashions.
Why discriminant?
As a result of they be taught a rule that instantly separates or predicts, with out modeling how the info was generated.
Earlier than this chapter, we already noticed fashions that had parameters, however they weren’t discriminant, they have been generative.
Allow us to recap rapidly.
- Choice Bushes use splits, or guidelines, and so there are not any weights to be taught. So they’re non-parametric fashions.
- k-NN shouldn’t be a mannequin. It retains the entire dataset and makes use of distances at prediction time.
Nevertheless, once we transfer from Euclidean distance to Mahalanobis distance, one thing fascinating occurs…
LDA and QDA do estimate parameters:
- means of every class
- covariance matrices
- priors
These are actual parameters, however they aren’t weights.
These fashions are generative as a result of they mannequin the density of every class, after which use it to make predictions.
So although they’re parametric, they don’t belong to the weight-based household.
And as you’ll be able to see, these are all classifiers, and so they estimate parameters for every class.

Linear Regression is our first instance of a mannequin that learns weights to construct a prediction.
That is the start of a brand new household within the Creation Calendar:
fashions that depend on weights + a loss perform to make predictions.
The Value Operate
How can we acquire the parameters a and b?
Effectively, the optimum values for a and b are these minimizing the price perform, which is the Squared Error of the mannequin.
So for every knowledge level, we will calculate the Squared Error.
Squared Error = (prediction-real worth)²=(a*x+b-real worth)²
Then we will calculate the MSE, or Imply Squared Error.
As we will see in Excel, the trendline provides us the optimum coefficients. When you manually change these values, even barely, the MSE will enhance.
That is precisely what “optimum” means right here: some other mixture of a and b makes the error worse.

The basic closed-form answer
Now that we all know what the mannequin is, and what it means to attenuate the squared error, we will lastly reply the important thing query:
How can we compute the 2 coefficients of Linear Regression, the slope a and the intercept b?
There are two methods to do it:
- the actual algebraic answer, generally known as the closed-form answer,
- or gradient descent, which we’ll discover simply after.
If we take the definition of the MSE and differentiate it with respect to a and b, one thing lovely occurs: the whole lot simplifies into two very compact formulation.

These formulation solely use:
- the common of x and y,
- how x varies (its variance),
- and the way x and y fluctuate collectively (their covariance).
So even with out understanding any calculus, and with solely primary spreadsheet features, we will reproduce the precise answer utilized in statistics textbooks.
The way to interpret the coefficients
For one characteristic, interpretation is simple and intuitive:
The slope a
It tells us how a lot y modifications when x will increase by one unit.
If the slope is 1.2, it means:
“when x goes up by 1, the mannequin expects y to go up by about 1.2.”
The intercept b
It’s the predicted worth of y when x = 0.
Typically, x = 0 doesn’t exist in the actual context of the info, so the intercept shouldn’t be at all times significant by itself.
Its position is usually to place the road appropriately to match the middle of the info.
That is normally how Linear Regression is taught:
a slope, an intercept, and a straight line.
With one characteristic, interpretation is straightforward.
With two, nonetheless manageable.
However as quickly as we begin including many options, it turns into tougher.
Tomorrow, we’ll focus on additional in regards to the interpretation.
At the moment, we’ll do the gradient descent.
Gradient Descent, Step by Step
After seeing the basic algebraic answer for Linear Regression, we will now discover the opposite important software behind fashionable machine studying: optimization.
The workhorse of optimization is Gradient Descent.
Understanding it on a quite simple instance makes the logic a lot clearer as soon as we apply it to Linear Regression.
A Light Heat-Up: Gradient Descent on a Single Variable
Earlier than implementing the gradient descent for the Linear Regression, we will first do it for a easy perform: (x-2)^2.
Everybody is aware of the minimal is at x=2.
However allow us to faux we have no idea that, and let the algorithm uncover it by itself.
The thought is to seek out the minimal of this perform utilizing the next course of:
- First, we randomly select an preliminary worth.
- Then for every step, we calculate the worth of the by-product perform df (for this x worth): df(x)
- And the subsequent worth of x is obtained by subtracting the worth of by-product multiplied by a step measurement: x = x – step_size*df(x)
You possibly can modify the 2 parameters of the gradient descent: the preliminary worth of x and the step measurement.
Sure, even with 100, or 1000. That’s fairly shocking to see, how effectively it really works.

However, in some circumstances, the gradient descent is not going to work. For instance, if the step measurement is just too massive, the x worth can explode.

Gradient descent for linear regression
The precept of the gradient descent algorithm is similar for linear regression: we’ve got to calculate the partial derivatives of the price perform with respect to the parameters a and b. Let’s be aware them as da and db.
Squared Error = (prediction-real worth)²=(a*x+b-real worth)²
da=2(a*x+b-real worth)*x
db=2(a*x+b-real worth)

After which, we will do the updates of the coefficients.

With this tiny replace, step-by-step, the optimum worth can be discovered after a number of interations.
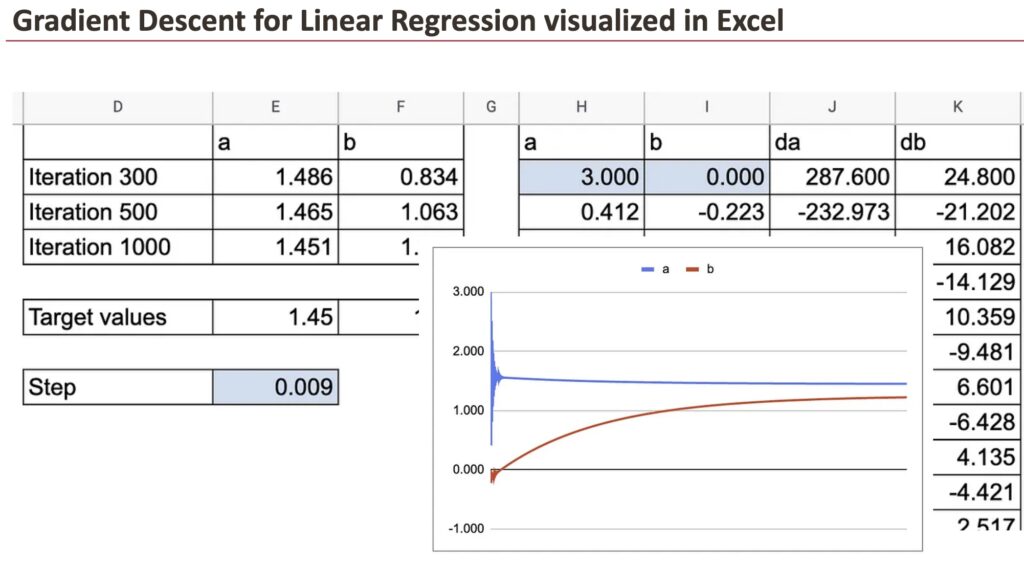
Within the following graph, you’ll be able to see how a and b converge in the direction of the goal worth.

We will additionally see all the small print of y hat, residuals and the partial derivatives.
We will absolutely admire the great thing about gradient descent, visualized in Excel.
For these two coefficients, we will observe how fast the convergence is.

Now, in observe, we’ve got many observations and this needs to be carried out for every knowledge level. That’s the place issues turn into loopy in Google Sheet. So, we use solely 10 knowledge factors.
You will notice that I first created a sheet with lengthy formulation to calculate da and db, which comprise the sum of the derivatives of all of the observations. Then I created one other sheet to indicate all the small print.
Conclusion
Linear Regression might look easy, however it introduces virtually the whole lot that fashionable machine studying depends on.
With simply two parameters, a slope and an intercept, it teaches us:
- the way to outline a value perform,
- the way to discover optimum parameters, numerically,
- and the way optimization behaves once we regulate studying charges or preliminary values.
The closed-form answer exhibits the class of the arithmetic.
Gradient Descent exhibits the mechanics behind the scenes.
Collectively, they type the muse of the “weighted + loss perform” household that features Logistic Regression, SVM, Neural Networks, and even immediately’s LLMs.
New Paths Forward
Chances are you’ll assume Linear Regression is straightforward, however with its foundations now clear, you’ll be able to prolong it, refine it, and reinterpret it by many alternative views:
- Change the loss perform
Exchange squared error with logistic loss, hinge loss, or different features, and new fashions seem. - Transfer to classification
Linear Regression itself can separate two courses (0 and 1), however extra strong variations result in Logistic Regression and SVM. And what about multiclass classification? - Mannequin nonlinearity
By means of polynomial options or kernels, linear fashions out of the blue turn into nonlinear within the unique area. - Scale to many options
Interpretation turns into more durable, regularization turns into important, and new numerical challenges seem. - Primal vs twin
Linear fashions could be written in two methods. The primal view learns the weights instantly. The twin view rewrites the whole lot utilizing dot merchandise between knowledge factors. - Perceive fashionable ML
Gradient Descent, and its variants, are the core of neural networks and enormous language fashions.
What we discovered right here with two parameters generalizes to billions.
Every little thing on this article stays throughout the boundaries of Linear Regression, but it prepares the bottom for a whole household of future fashions.
Day after day, the Creation Calendar will present how all these concepts join.