, the order of phrases is key to which means. The phrases “the canine chased the cat” and “the cat chased the canine” use the very same phrases, however their sequence conveys solely totally different occasions. Nevertheless, the Transformer structure, which powers most fashionable language fashions, processes all enter tokens in parallel. This parallel processing makes it extremely environment friendly but additionally inherently blind to the order of the tokens. And not using a mechanism to know sequence, the mannequin would deal with a sentence like an unordered bag of phrases.
To unravel this, positional embeddings had been launched. These are vectors that present the mannequin with specific details about the place of every token within the sequence. By combining token embeddings with positional embeddings, the mannequin can study to leverage phrase order and perceive the contextual relationships that depend upon it.
This text gives a mathematical deep dive into three pivotal positional embedding strategies, full with code examples to solidify your understanding. We’ll discover:
- Absolute Positional Embeddings (APE): The unique sinusoidal methodology proposed within the “Consideration Is All You Want” paper, which assigns a singular positional vector to every absolute place. [2]
- Rotary Place Embedding (RoPE): A sublime strategy that includes relative positional info by rotating the question and key vectors within the consideration mechanism. [4]
- Consideration with Linear Biases (ALiBi): A easy but efficient approach that avoids including embeddings altogether, as an alternative biasing the eye scores based mostly on the gap between tokens. [5]
To construct a strong basis, let’s first start with the constructing block for the unique positional encoding: the sinusoidal wave.
Sinusoidal Wave
Let’s begin with understanding the sinusoidal wave (determine 1). Right here (omega) is the angular frequency, (u) is the unit towards which the wave is tracked and (phi_0) is the preliminary part fixed (typically set to 0 in embeddings). The unit (u) will be distance (measured in metres), time (measured in seconds) or for embeddings – the place. Angular frequency measures the quantity by which the part or the angle modifications per unit (u).
[displaystyle
y = sin(omega u + phi_0) tag{1}
]
Wavelength ((lambda)) is the gap between any two consecutive peaks or any two troughs (lowest factors of the wave), which means that when a wave has travelled a distance of wavelength, we now have one full rotation (2*(pi)).
The next block derives the connection between the wavelength and the angular frequency and it reveals that they’re inversely proportional. From this inverse relation we are able to infer that when the angular frequency is excessive, the speed of oscillation is excessive, for the reason that wavelength is small and the wave repeats inside a brief distance and when the angular frequency is low, the speed of oscillation is low, which means the wave’s place is sort of unchanged.
[displaystyle
begin{aligned}
y(u+lambda) &= y(u)
sin!big(omega(u+lambda)+phi_0big) &= sin(omega u+phi_0)
sin(omega u+phi_0+omegalambda) &= sin(omega u+phi_0)
end{aligned}
]
[displaystyle
text{LHS = RHS only if } omegalambda = 2pi n,quad ninmathbb{Z}.
]
[displaystyle
text{Since }lambdatext{ is the distance between consecutive peaks/troughs, set }n=1
Rightarrow
lambda = frac{2pi}{omega}. tag{2}
]
With this understanding of the sine wave, we are actually able to know “Absolute Positional Embeddings”
Absolute Positional Embeddings
Absolute Positional Embeddings (APE) was first launched within the “Consideration Is All You Want” [2] paper and this varieties the idea both immediately or not directly for lots of the positional embedding strategies which are used immediately. On this part I’ll current an in depth mathematical background behind the formulation offered the paper. I’ll begin off with the precise formulation used within the paper (discuss with determine 2) after which proceed to interrupt it down. The equation might sound easy but it surely has so many helpful properties.

The variables used within the equation from the determine are:
- (pos) – place of a token within the given sequence
- (d_{mannequin}) – dimensionality of the place vector
- (i) – the (i_{th}) dimension of the place vector
Let’s evaluate how the equation compares with the standard sinusoidal wave
For a fair dimension (i), the sine curve is
[displaystyle
y_i(mathrm{pos}) ;=; sinleft(frac{mathrm{pos}}{10000^{frac{2i}{d_{mathrm{model}}}}}right)
;=; sinleft(frac{mathrm{pos}}{B_i}right). tag{3}
]
Evaluating equation (3) with equation (1), we get:
[displaystyle
omega ;=; frac{1}{B_i}. tag{4}
]
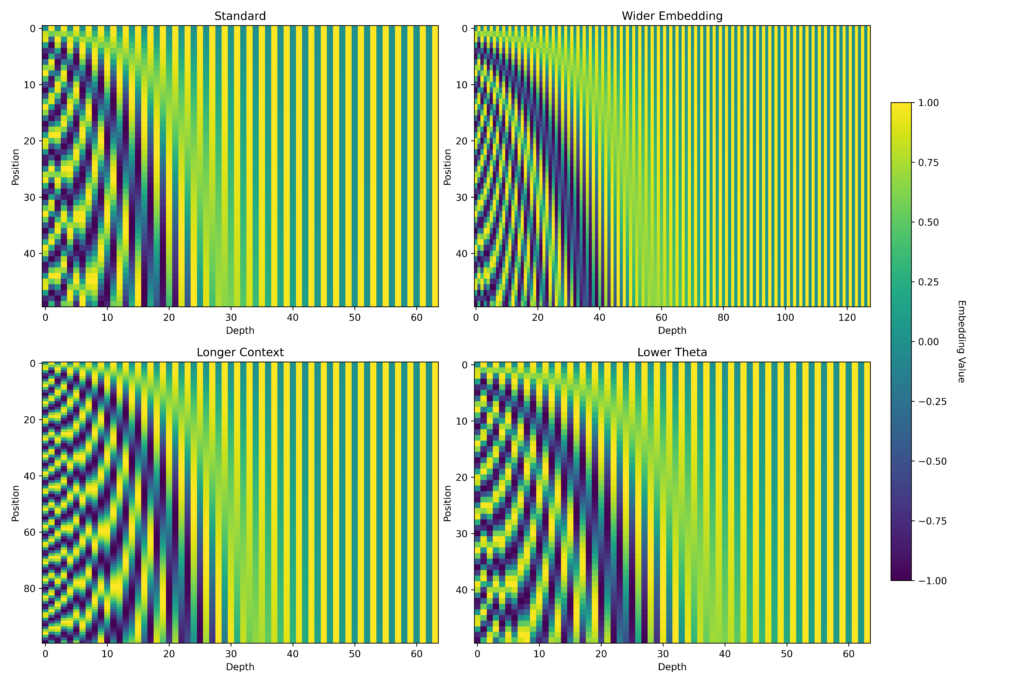
From equation 4, we are able to infer that as (i) will increase the angular frequency of the wave decreases, which means that at larger dimensions the values don’t change a lot between the positional vectors of two totally different positions. However at decrease dimensions the values change quickly. This can be a extremely helpful property as a result of inside a single vector we are able to encode each excessive frequency (decrease dimensions) and low frequency info (larger dimensions). We will show this by evaluating the cosine similarity of decrease dimension sub-vectors of adjoining positions and better dimension sub-vectors of adjoining positions. Readers can execute the code under to confirm it for themself:
import numpy as np
def get_pos_emb(theta, n_embd, ctx_size):
thetas = theta ** ((-2 * np.arange(0, n_embd // 2)) / n_embd) # n_embd // 2
pos = np.arange(ctx_size) # ctx_size
freqs = np.outer(pos, thetas) # ctx_size, n_embd // 2
even_pos = np.sin(freqs)
odd_pos = np.cos(freqs)
pos_emb = np.stack((even_pos, odd_pos), axis=2)
pos_emb = pos_emb.reshape(ctx_size, -1) # ctx_size, n_embd
return pos_emb
def cosine_similarity(vec1, vec2):
assert vec1.form == vec2.form
dot = np.dot(vec1, vec2)
mag1, mag2 = np.linalg.norm(vec1), np.linalg.norm(vec2)
return dot / (mag1 * mag2)
theta = 10000
n_embd = 32
ctx_size = 32
pos_emb = get_pos_emb(theta, n_embd, ctx_size)
l = 5
u = 27
print(f'decrease dims: {cosine_similarity(pos_emb[0, :l], pos_emb[1, :l])}')
print(f'larger dims: {cosine_similarity(pos_emb[0, u:], pos_emb[1, u:])}')
# output
# decrease dims: 0.6769
# larger dims: 0.9999At this level you might be like: “Okay, however how is this convenient?”, effectively I can clarify how it’s helpful in two methods. The primary rationalization is that the weights of the mannequin can study to affiliate the distinction within the decrease dimensions with the distinction within the place of the tokens and might study to affiliate the similarity within the larger dimensions with the lengthy vary dependency.
The second rationalization entails breaking down the eye mechanism, which is what I’ll be doing under 🙂
Contemplate two tokens at positions (m) and (n) respectively. Their embedding (x_m) and (x_n) are made up of the token embedding (w_{m,n}) and place embedding (p_{m,n}). The eye mechanism works by calculating the dot product between the question vector of (m) and the important thing vector of (n), which is damaged down equation 5.
[
begin{equation}
begin{aligned}
q^top k
&= (W_q x_m)^top (W_k x_n)
&= big(W_q(w_m+p_m)big)^top big(W_k(w_n+p_n)big)
&= (w_m^top W_q^top + p_m^top W_q^top)(W_k w_n + W_k p_n)
&= underbrace{w_m^top W_q^top W_k w_n}_{text{content–content}}
+ underbrace{big(w_m^top W_q^top W_k p_n + p_m^top W_q^top W_k w_nbig)}_{text{content–position}}
+ underbrace{p_m^top W_q^top W_k p_n}_{text{position–position}} .
end{aligned}
tag{5}
end{equation}
]
Since it is a weblog publish on the affect of place, the final time period in equation 5, the place the place embeddings work together is our fundamental focal point. From determine 2, we all know {that a} place embedding is made up of pairs of sin / cos waves, which type d/2 vectors of dimension 2. Within the following instance for simplicity we’ll contemplate one sin / cos pair and we’ll assume that the load matrices (W_q) and (W_k) are identification matrices, which ends up in simply vector dot product of (p_m) and (p_n). Equation 6 reveals the results of the dot product for the place vectors for any single sin / cos pair. We will see that the dot product is dependent upon the distinction between the place of the vectors. Generalizing this to a number of dimensions we get equation 6.
[
begin{equation}
begin{aligned}
mathbf{p}_m &= begin{bmatrix}
sin!left(frac{m}{B_i}right)[2pt]
cos!left(frac{m}{B_i}proper)
finish{bmatrix},quad
mathbf{p}_n = start{bmatrix}
sin!left(frac{n}{B_i}proper)[2pt]
cos!left(frac{n}{B_i}proper)
finish{bmatrix},
mathbf{p}_m^high mathbf{p}_n
&= sin!left(frac{m}{B_i}proper)sin!left(frac{n}{B_i}proper)
+ cos!left(frac{m}{B_i}proper)cos!left(frac{n}{B_i}proper)
&= cos!left(frac{m-n}{B_i}proper).
finish{aligned}
tag{6}
finish{equation}
]
[
begin{equation}
mathbf{p}_m^top mathbf{p}_n
= sum_{i=0}^{frac{d}{2}-1} cos!left(frac{m-n}{B_i}right).
tag{7}
end{equation}
]
And from equation 7, we are able to infer that top frequency pairs (small (B_i), decrease dimensions) are extremely delicate to modifications within the relative place whereas low frequency pairs (huge (B_i), larger dimensions) change slowly with the change in relative place which helps conserving the lengthy vary dependency. That is how having excessive frequency and low frequency parts inside the similar vector helps the mannequin find out about place and relative place.
I’d like to debate another property, which is that the place vector (p_{(m+t)}) is simply the pairwise clockwise rotation of the place vector (p_m) with every pair rotated by an angle ((t/B_i)). The proof is labored out in determine 6. We will simply lengthen this to the entire vector, the place the rotation matrix will likely be a sparse matrix with dimensions (d_{mannequin} x d_{mannequin}).
[
begin{equation}
begin{aligned}
mathbf{p}_m &=
begin{bmatrix}
sinleft(frac{m}{B_i}right)[2pt]
cosleft(frac{m}{B_i}proper)
finish{bmatrix},quad
mathbf{p}_{m+t} =
start{bmatrix}
sinleft(frac{m+t}{B_i}proper)[2pt]
cosleft(frac{m+t}{B_i}proper)
finish{bmatrix},[4pt]
mathbf{p}_{m+t}
&=
start{bmatrix}
sinleft(frac{m}{B_i}proper)cosleft(frac{t}{B_i}proper)
+cosleft(frac{m}{B_i}proper)sinleft(frac{t}{B_i}proper)
cosleft(frac{m}{B_i}proper)cosleft(frac{t}{B_i}proper)
-sinleft(frac{m}{B_i}proper)sinleft(frac{t}{B_i}proper)
finish{bmatrix}
&=
underbrace{
start{bmatrix}
cosleft(frac{t}{B_i}proper) & sinleft(frac{t}{B_i}proper)
-sinleft(frac{t}{B_i}proper) & cosleft(frac{t}{B_i}proper)
finish{bmatrix}
}_{Rleft(frac{t}{B_i}proper)}
start{bmatrix}
sinleft(frac{m}{B_i}proper)
cosleft(frac{m}{B_i}proper)
finish{bmatrix}
= Rleft(frac{t}{B_i}proper)mathbf{p}_m .
finish{aligned}
tag{8}
finish{equation}
]
In the event you take a pair of dimensions (even, odd) and plot them in a 2-dimensional aircraft, you’re going to get a pleasant circle due to the rotation property.

In my second rationalization on the usefulness of getting excessive frequency and low frequency pairs, we made one small however necessary simplification which is assuming that the load matrices had been identification matrices. If we take away this simplification, we’ll nonetheless have the benefits we mentioned on this part however we may also have absolute items blended within the calculation which don’t contribute to the eye mechanism. So to this finish, we want the equation 5 to look one thing like equation 9, which simply accommodates the content-content info and the place / relative place info. That is the place RoPE [4], is available in, which is mentioned intimately within the subsequent part.
[
begin{equation}
q^top k ;=; w_m^top W_q^top W_k, w_n ;+; g(n-m).
tag{9}
end{equation}
]
Rotary Place Embedding (RoPE)
Okay, we now know the way APE works, why is it good and why it’s not nice. From the concluding paragraph of the earlier part, we all know that we’d like a formulation the place we’re solely involved concerning the relative place between the tokens and never absolutely the place of them. To get such a formulation the authors of RoPE [4], proposed the next set of equations as the answer:
[
begin{equation}
begin{aligned}
q_m &= R(theta, m), W_q, x_q,
k_n &= R(theta, n), W_k, x_k,
q_m^top k_n &= (W_q x_q)^top, R(theta, n – m), (W_k x_k).
end{aligned}
tag{10}
end{equation}
]
As you’ll be able to see in equation 10, we get a query-key dot product that relies upon solely on the relative place of the tokens (by means of the rotation matrix (R), defined under) and their semantic content material (the token embeddings), which removes absolutely the place leakage and the interplay between absolutely the place and semantic content material that was current in APE (determine 3).
Notice: I’ll solely be discussing the properties of the RoPE embedding and I gained’t be deriving it right here, as a result of attempting to signify all of the equations right here turned fairly laborious. So for readers, I wrote a latex doc that accommodates the derivation — here.
So what’s ‘R’ in equation 10? ‘R’ is a rotation matrix that rotates a vector and the angle by which it rotates is dependent upon the place of the vector within the sequence. For a two dimensional vector at place (n), (R) is proven in equation 11. So how can we lengthen to greater than two dimensions ie how can we rotate a d-dimensional vector? The authors take inspiration from the APE paper the place every pair of dimensions are rotated, resulting in a sparse matrix which is represented in equation 12.
[
begin{equation}
R(theta,n)=
begin{bmatrix}
cos(ntheta) & -sin(ntheta)
sin(ntheta) & cos(ntheta)
end{bmatrix}.
tag{11}
end{equation}
]
[
begin{equation}
R(theta,n)=mathrm{blkdiag}!big(R(ntheta_1),R(ntheta_2),ldots,R(ntheta_L)big)inmathbb{R}^{2Ltimes 2L},
quadtext{where }
R(ntheta_i)=
begin{bmatrix}
cos(ntheta_i) & -sin(ntheta_i)
sin(ntheta_i) & cos(ntheta_i)
end{bmatrix}.
tag{12}
end{equation}
]
The rotation matrix can be an orthogonal matrix which ensures coaching stability as a result of it doesn’t shrink or enlarge the gradient vector throughout backpropagation. The sparsity of the matrix additionally makes the rotation of the vector computationally simpler.
Given under is a self-contained implementation of RoPE for readers who’ve gone by means of my derivation and are questioning the right way to implement it. The instinct behind this code and the way in which it’s written (I carried out mine by referring to LLaMA’s code base) is so stunning which I feel wants a separate weblog publish in itself. Explaining it right here would make the weblog publish huge and so I resist myself:)
def get_freqs_cis(theta, n_embd, n_heads, ctx_size) -> Tensor:
head_dim = n_embd // n_heads
i = torch.arange(head_dim // 2)
thetas = theta ** (-2 * i / head_dim) # head_dim // 2
pos = torch.arange(ctx_size) # pos
freqs = torch.outer(pos, thetas) # pos, head_dim // 2
actual = torch.cos(freqs)
imag = torch.sin(freqs)
return torch.advanced(actual, imag)
def apply_rot_emb(x: Tensor, freqs: Tensor) -> Tensor:
# x -> bsz, n_heads, seq_len, head_dim; freqs -> pos, head_dim // 2
bsz, n_heads, seq_len, head_dim = x.form
half = head_dim // 2
f = freqs[:seq_len]
x = x.reshape(bsz, n_heads, seq_len, half, 2)
x_rot = torch.view_as_complex(x) * f.view(1, 1, seq_len, half) # bsz, n_heads, seq_len, head_dim // 2
x_real = torch.view_as_real(x_rot) # bsz, n_heads, seq_len, head_dim // 2, 2
return x_real.reshape(bsz, n_heads, seq_len, head_dim)Consideration with Linear Biases (ALiBi):
If the readers had diligently gone by means of the code snippets for each APE and RoPE, then a query that might have naturally risen is, what if we transcend the context window throughout inference? Since each APE and RoPE are static, we all know that the positional embeddings will be prolonged past the context window however do they carry out effectively? That is what the authors of ALiBi [5] discover and likewise suggest ALiBi that performs higher than APE and RoPE once we transcend the context window throughout inference and likewise trains sooner than RoPE.
After going by means of math intense positional embedding sorts, ALiBi ought to be simpler to know and after you undergo the experiments part, additionally, you will have the ability to respect ALiBi and Occam’s Razor.
ALiBI doesn’t add positional embeddings to the token embeddings like APE or rotates the token embeddings to inject positional info like RoPE relatively it introduces recency bias to sure heads whereas sustaining long run dependency to different heads by including a static matrix to the eye matrix of every head. That is proven visually in determine 4, the place (m) known as the ‘slope’ whose worth modifications based mostly on the eye head. As you’ll be able to see from the determine, as the gap between two tokens will increase the penalty on the dot product will increase; even RoPE has this good property the place the dot product between distant vectors are smaller than the dot product between close by vectors and it’s referred to as long run decay which is one other necessary property of RoPE and ALiBi as effectively.

To determine the worth of ‘m’ for a selected head the authors use a easy geometric development which has each the beginning and the ratio as (2^{-8/n_{heads}}), the place n is the variety of consideration heads. The authors additionally experimented with making ‘m’ learnable however the outcomes confirmed that it didn’t present them with good extrapolation outcomes. Given under is the code implementation for ALiBi and it’s simply replicating determine 4 in PyTorch code.
def get_alibi_slopes(n_heads) -> Tensor:
begin = 2 ** (-8 / n_heads)
ratio = begin
return torch.tensor([start * (ratio ** i) for i in range(n_heads)])
def get_linear_bias(n_heads, ctx_size) -> Tensor:
slopes = get_alibi_slopes(n_heads).view(n_heads, 1, 1)
pos = torch.arange(ctx_size)
distances = pos[None, :] - pos[:, None]
distances = torch.the place(distances > 0, 0, distances) # ctx_size, ctx_size
distances.unsqueeze_(0) # 1, ctx_size, ctx_size
linear_bias = distances * slopes # n_heads, ctx_size, ctx_size
return linear_bias.unsqueeze(0) # 1, n_heads, ctx_size, ctx_sizeExperiments
After going by means of all the speculation, it’s at all times greatest to implement these various kinds of embeddings, prepare language fashions that makes use of various kinds of positional embeddings and evaluate them on sure metrics. I’ve supplied the entire code for the experiments on this repo - https://github.com/SkAndMl/llama and the outcomes of my experiments on TinyStories dataset [6] (CDLA-Sharing-1.0 LICENSE) are given under. I urge the readers to obtain the code and prepare the totally different fashions regionally as it would additionally provide you with a really feel of coaching language fashions.
Figures 5 and 6 present the coaching loss, validation loss, perplexity and time taken to coach 28M parameter LLaMA impressed language mannequin with 4 heads, 4 layers, 256 context dimension and 256 embedding dimension on an M2 Macbook Professional laptop computer. All of the fashions had been skilled for 1000 steps and used a batch dimension of 32. As you’ll be able to see each ALiBi and RoPE have related performances and are significantly better than APE which has to take care of “further phrases” within the consideration mechanism. One distinct benefit that ALiBi has over RoPE is that it’s sooner to coach fashions utilizing ALiBi as will be seen from determine 6. To be sincere, I can present no theoretical rationalization or instinct behind why one carried out higher than the opposite since any deep studying concept presently can solely be validated by way of experiments.


Conclusion
Oh god, I had a lot enjoyable writing this text, studying about positional embeddings, coding them and understanding the mathematics behind them. This took me a few month to write down and it helped me perceive loads about positional embeddings. I hope you guys take pleasure in it too. Cheers!
References:
1. https://medium.com/autonomous-agents/math-behind-positional-embeddings-in-transformer-models-921db18b0c28
2. Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Consideration is all you want. In Proceedings of the thirty first Worldwide Convention on Neural Data Processing Methods (NIPS’17). Curran Associates Inc., Pink Hook, NY, USA, 6000–6010.
3. Sine wave — https://simple.wikipedia.org/wiki/Sine_wave
4. Su, J., Lu, Y., Pan, S., Wen, B., & Liu, Y. (2021). RoFormer: Enhanced Transformer with Rotary Place Embedding. ArXiv, abs/2104.09864.
5. Press, Ofir, Noah A. Smith, and Mike Lewis. “Prepare quick, take a look at lengthy: Consideration with linear biases permits enter size extrapolation.” arXiv preprint arXiv:2108.12409 (2021).
6. TinyStories dataset: https://huggingface.co/datasets/roneneldan/TinyStories