One may encounter quite a few irritating difficulties when attempting to numerically clear up a troublesome nonlinear and nonconvex optimum management drawback. On this article I’ll take into account such a troublesome drawback, that of discovering the shortest path between two factors by an impediment discipline for a widely known mannequin of a wheeled robotic. I’ll look at widespread points that come up when attempting to resolve such an issue numerically (particularly, nonsmoothness of the associated fee and chattering within the management) and how one can deal with them. Examples assist to make clear the ideas. Get all of the code right here: https://github.com/willem-daniel-esterhuizen/car_OCP
1.1 Define
First, I’ll introduce the automobile mannequin that we’ll examine all through the article. Then, I’ll state the optimum management drawback in all its element. The following part then exposes all of the numerical difficulties that come up, ending with a “smart nonlinear programme” that makes an attempt to take care of them. I’ll then current the small print of a homotopy technique, which helps in guiding the solver in the direction of an excellent answer. I’ll then present you some numerical experiments to make clear every thing, and end off with references for additional studying.
2. A automobile mannequin
We’ll take into account the next equations of movement,
[
begin{align}
dot x_1(t) &= u_1(t)cos(x_3(t)),
dot x_2(t) &= u_1(t)sin(x_3(t)),
dot x_3(t) &= u_2(t),
end{align}
]
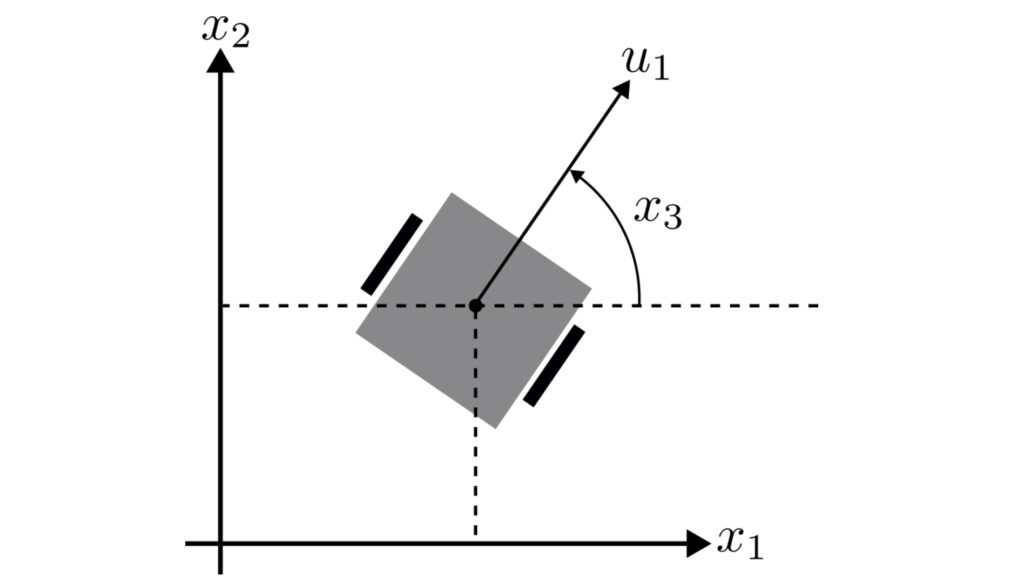
the place (t geq 0) denotes time, (x_1inmathbb{R}) and (x_2inmathbb{R}) denote the automobile’s place, (x_3inmathbb{R}) denotes its orientation, (u_1inmathbb{R}) its velocity and (u_2inmathbb{R}) its charge of turning. This can be a widespread mannequin of a differential-drive robotic, which consists of two wheels that may flip independently. This permits it to drive forwards and backwards, rotate when stationary and carry out different elaborate driving manoeuvres. Word that, as a result of (u_1) may be 0, the mannequin permits the automobile to cease instantaneously.
All through the article we’ll let (mathbf{x} := (x_1, x_2, x_3)^topinmathbb{R}^3) denote the state, (mathbf{u} := (u_1, u_2)inmathbb{R}^2) denote the management, and outline (f:mathbb{R}^3timesmathbb{R}^2 rightarrow mathbb{R}^3) to be,
[
f(mathbf{x},mathbf{u}) :=
left(
begin{array}{c}
u_1cos(x_3)
u_1sin(x_3)
u_2
end{array}
right),
]
in order that we are able to succinctly write the system as,
[
dot{mathbf{x}}(t) = f(mathbf{x}(t), mathbf{u}(t)),quad tgeq 0.
]
3. Optimum path planning drawback
Contemplating the automobile mannequin within the earlier part, we wish to discover the shortest path connecting an preliminary and goal place whereas avoiding quite a few obstacles. To that finish, we’ll take into account the next optimum management drawback:
[
newcommand{u}{mathbf{u}}
newcommand{x}{mathbf{x}}
newcommand{PC}{mathrm{PC}}
newcommand{C}{mathrm{C}}
newcommand{mbbR}{mathbb{R}}
newcommand{dee}{mathrm{d}}
newcommand{NLP}{mathrm{NLP}}
mathrm{OCP}:
begin{cases}
minlimits_{x, u} quad & J(x, u)
mathrm{subject to:}quad & dot{x}(t) = f(x(t),u(t)), quad & mathrm{a.e.},, t in[0,T], &
quad & x(0) = x^{mathrm{ini}}, & &
quad & x(T) = x^{mathrm{tar}}, & &
quad & u(t) in mathbb{U}, quad & mathrm{a.e.},, t in[0,T], &
quad & (x_1(t) – c_1^i)^2 + (x_2(t) – c_2^i)^2 geq r_i^2, quad & forall tin[0,T],, forall iin mathbb{I}, &
quad & (x, u) in C_T^3timesPC_T^2,
finish{circumstances}
]
the place (Tgeq 0) is the finite time horizon, (J:C_T^3timesPC_T^2rightarrow mbbR_{geq 0}) is the associated fee purposeful, (x^{mathrm{ini}} inmbbR^3) is the preliminary state and (x^{mathrm{tar}}inmbbR^3) is the goal state. The management is constrained to (mathbb{U}:= [underline{u}_1, overline{u}_1]instances [underline{u}_2, overline{u}_2]), with (underline{u}_j < 0 <overline{u}_j), (j=1,2). Round obstacles are given by a centre, ((c_1^i, c_2^i)inmbbR^2), and a radius, (r_iinmbbR_{geq 0}), with (mathbb{I}) indicating the indices of all obstacles. For the associated fee purposeful we’ll take into account the arc size of the curve connecting (x^{mathrm{ini}}) and (x^{mathrm{tar}}), that’s,
[
J(x,u) = int_0^Tleft(dot x_1^2(s) + dot x_2^2(s)right)^{frac{1}{2}}, dee s.
]
I’ve use the short-hand (PC_T^m) (respectively (C_T^m)) to indicate all piece-wise steady features (respectively steady features) mapping the interval ([0,T]) to (mbbR^m). The acronym “(mathrm{a.e.},, t in[0,T])” stands for “nearly each t in ([0,T])”, in different phrases, the spinoff might not exist at a finite variety of factors in ([0,T]), for instance, the place the management is discontinuous.
3.1 Some feedback on the OCP
The equations of movement and the presence of obstacles make the optimum management drawback nonlinear and nonconvex, which is troublesome to resolve basically. A solver might converge to regionally optimum options, which aren’t essentially globally optimum, or it could fail to discover a possible answer though one exists.
For simplicity the obstacles are circles. These are good as a result of they’re differentiable, so we are able to use a gradient-based algorithm to resolve the OCP. (We’ll use IPOPT, which implements an interior-point technique.) The arc size perform, (J), is not differentiable when the automobile’s velocity is zero. Nevertheless, as we’ll see, we are able to get rid of this drawback by including a small (varepsilon > 0) beneath the square-root.
Relying on the scheme used to discretise the equations of movement, there could also be chattering within the management sign. As we’ll see, this may simply be handled by penalising extreme management motion in the associated fee perform.
The horizon size thought of in the issue, (T), is mounted. Thus, as the issue is posed, we truly wish to discover the curve of shortest arc size for which the automobile reaches the goal in precisely (T) seconds. That is truly not a difficulty for our automobile as a result of it could actually cease instantaneously and rotate on the spot. So, the options to the OCP (if the solver can discover them) may include lengthy boring chunks at first and/or finish of the time interval if (T) could be very massive. If we needed to make the horizon size a call variable in the issue then now we have two choices.
First, if we use a direct technique to numerically clear up the issue (as we are going to do within the subsequent part) we might fluctuate the horizon size by making the discretisation step dimension (h), which seems within the numerical integration scheme, a call variable. It’s because the dimension of the choice house should be set on the time at which you invoke the numerical nonlinear programme solver.
The second possibility is to resort to an oblique technique (in a nutshell, it’s essential to clear up a boundary-value drawback that you simply get from an evaluation of the issue through Pontryagin’s precept, typically through the capturing technique). Nevertheless, for an issue like ours, the place you will have many state constraints, this may be fairly troublesome.
In case you are discovering this text fascinating, please take into account testing the weblog topicincontrol.com. It presents deep dives into management concept, optimization, and associated subjects, typically with freely accessible code.
4. Deriving a smart nonlinear programme
We’ll clear up the optimum management drawback utilizing direct single capturing. Extra exactly, we’ll take the management to be piecewise fixed over a uniform grid of time intervals and propagate the state trajectory from the preliminary situation utilizing the fourth-order Runge-Kutta (RK4) technique. We’ll then type a finite-dimensional nonlinear programme (NLP), the place the choice variables include the state and management at every discrete time step. This part reveals how one can type a “smart” NLP, which offers with the varied numerical difficulties.
4.1 The RK4 scheme
Contemplate the automobile’s differential equation, with preliminary situation, (x^{mathrm{ini}}), over an interval, ([0,T]),
[
dot{x}(t) = f(x(t), u(t)), quad tin[0,T], quad x(0) = x^{mathrm{ini}}.
]
Let (h>0) denote the fixed time step, and let (Okay := mathrm{flooring}(T/h)). Then the RK4 scheme reads,
[
x[k+1] = x[k] + frac{h}{6}mathrm{RK}_4(x[k], u[k]), quad forall ,, ok in[0:K-1], quad x[0] = x(0),
]
the place (mathrm{RK}_4:mbbR^3times mbbR^2 rightarrow mbbR^3) reads,
[
mathrm{RK}_4(x, u) = k_1 + 2k_2 + 2k_3 + k_4,
]
and
[
k_1 = f(x, u),quad k_2 = f(x+ frac{h}{2}k_1, u), quad k_3 = f(x + frac{h}{2}k_2, u),quad k_4 = f(x + hk_3, u).
]
The notation (x[k]) and (u[k]) is supposed to indicate the discretised state and management, respectively, in order to tell apart them from their continuous-time counterparts.
4.2 Singularity of the associated fee purposeful
You is likely to be tempted to contemplate the polygonal arc size as the associated fee within the NLP, particularly,
[
sum_{k=0}^{K-1}Vertx[k+1] – x[k]Vert = sum_{ok=0}^{Okay-1}left((x_{1}[k+1] – x_1[k])^2 + (x_2[k+1] – x_2[k])^2right)^{frac{1}{2}}.
]
Nevertheless, this perform is not differentiable if for some (kin{0,1,dots,Okay-1}),
[
Vertx[k+1] – x[k]Vert = 0,
]
which regularly results in the solver failing. You may see the error EXIT: Invalid quantity in NLP perform or spinoff detected when you clear up an issue with this text’s code (which makes use of IPOPT, a gradient-based solver).
One answer is to approximate the polygonal arc size with,
[
sum_{k=0}^{K-1}left((x_{1}[k+1] – x_1[k])^2 + (x_2[k+1] – x_2[k])^2 + varepsilonright)^{frac{1}{2}},
]
with (varepsilon > 0) a small quantity. We see that, for an arbitrary (kin{1,dots,Okay-1}) and (iin{1,2}),
[
begin{align*}
frac{partial}{partial x_i[k]} &left( sum_{m=0}^{Okay-1} left(x_1[m+1] – x_1[m])^2 + (x_2[m+1] – x_2[m])^2 + varepsilonright)^{frac{1}{2}} proper) [6pt]
&= frac{x_i[k] – x_i[k-1]}{left((x_1[k] – x_1[k-1])^2 + (x_2[k] – x_2[k-1])^2 + varepsilonright)^{frac{1}{2}}}
&quad + frac{x_i[k] – x_i[k+1]}{left((x_1[k+1] – x_1[k])^2 + (x_2[k+1] – x_2[k])^2 + varepsilon proper)^{frac{1}{2}}}
finish{align*}
]
and so this perform is constantly differentiable, guaranteeing clean gradients for IPOPT. (You get related expressions when you have a look at (frac{partial}{partial x_i[K]}) and (frac{partial}{partial x_i[0]})).
4.3 Management chattering
Management chattering is the fast leaping/oscillation/switching of the optimum management sign. There could also be elements of the answer that actually chatter (this may increasingly happen when the optimum management is bang-bang, for instance) or a numerical solver might discover a answer that chatters artificially. Delving into this deep matter is out of this text’s scope however, very briefly, you may encounter this phenomenon in issues the place the optimum answer reveals so-called lively arcs. These are parts of the answer alongside which the state constraints are lively, which, in our setting, corresponds to the automobile travelling alongside the boundaries of the obstacles alongside its optimum path. When fixing issues exhibiting such arcs through a direct technique, as we’re doing, the numerical solver might approximate the true answer alongside these arcs with fast oscillation.
Fortunately, a easy option to do away with chattering is to only penalise management motion by including the time period:
[
deltasum_{k=0}^{K-1}Vert u[k] Vert^2
]
in the associated fee perform, for some small (delta). (This at the least works properly for our drawback, even for very small (delta).)
4.4 Scaling for good numerical conditioning
A well-scaled nonlinear programme is one the place small modifications within the determination variable end in small modifications in the associated fee and the values of the constraint features (the so-called constraint residuals). We are able to test how properly our drawback is scaled by trying on the magnitude of the associated fee perform, at its gradient and Hessian, as properly the Jacobian of the constraint perform at factors within the determination house (in particuar, on the preliminary heat begin and factors near the answer). If these portions are of comparable order then the solver shall be strong, which means it should normally converge in comparatively few steps. A badly-scaled drawback might take extraordinarily lengthy to converge (as a result of it’d have to take very small steps of the choice variable) or just fail.
Contemplating our drawback, it is smart to scale the associated fee by roughly the size we anticipate the ultimate path to be. A good selection is the size of the road connecting the preliminary and goal positions, name this (L). Furthermore, it then is smart to scale the constraints by (1/L^2) (as a result of we’re squaring portions right here).
4.5 The smart nonlinear programme
Taking the discussions of the earlier subsections under consideration, the smart NLP that we’ll take into account within the numerics part reads,
[
NLP_{varepsilon, delta}:
begin{cases}
minlimits_{x, u} quad & J_{varepsilon,delta}(x, u)
mathrm{subject to:}
quad & x[k+1] = x[k] + frac{h}{6}mathrm{RK}_4(x[k], u[k]), & forall ok in[0:K-1], &
quad & x[0] = x^{mathrm{ini}}, &
quad & x[K] = x^{mathrm{tar}}, &
quad & u[k]in mathbb{U}, & forall ok in[0:K-1], &
quad & frac{1}{L^2}left( x_1[k] – c_1^i proper)^2 + frac{1}{L^2}left( x_2[k] – c_2^i proper)^2 geq frac{1}{L^2} r_i^2, quad & forall ok in[0:K], & forall iin mathbb{I},
quad & (x, u) in (mbbR^{3})^Okay instances (mbbR^{2})^{Okay-1}, &
finish{circumstances}
]
the place (J_{varepsilon,delta}: (mbbR^{3})^Okay instances (mbbR^{2})^{Okay-1} rightarrow mbbR_{>0}) is outlined to be,
[
J_{varepsilon,delta}(x, u) := frac{1}{L} left(sum_{k=0}^{K-1}left(Vert x[k+1] – x[k]Vert^2 + varepsilon proper)^{frac{1}{2}} + deltasum_{ok=0}^{Okay-1}Vert u[k] Vert^2 proper).
]
To assist upcoming dialogue, outline the possible set, (Omega), to be the set of all pairs ((x,u)) that fulfill the constraints of (NLP_{varepsilon, delta}). A possible pair ((x^{(varepsilon,delta)}, u^{(varepsilon,delta)})) is claimed to be globally optimum offered that,
[
J_{varepsilon,delta}(x^{(varepsilon,delta)}, u^{(varepsilon,delta)}) leq J_{varepsilon,delta}(x, u),quadforall(x, u) in Omega.
]
A possible pair ((x^{(varepsilon,delta)}, u^{(varepsilon,delta)})) is claimed to be regionally optimum offered that there exists a sufficiently small (gamma >0) for which,
[
J_{varepsilon,delta}(x^{(varepsilon,delta)}, u^{(varepsilon,delta)}) leq J_{varepsilon,delta}(x, u),quadforall(x, u) in Omegacap mathbf{B}_{gamma}(x^{(varepsilon,delta)}, u^{(varepsilon,delta)}).
]
Right here (mathbf{B}_{gamma}(x^{(varepsilon,delta)}, u^{(varepsilon,delta)}) ) denotes a Euclidean ball of radius (gamma>0) centred concerning the level ((x^{(varepsilon,delta)}, u^{(varepsilon,delta)}) ).
5. A homotopy technique
Recall that the issue is nonlinear and nonconvex. Thus, if we had been to only select a small (varepsilon>0) and (delta>0) and throw (NLP_{varepsilon, delta}) at a solver, then it might fail though possible pairs may exist, or it could discover “unhealthy” regionally optimum pairs. One method to take care of these points is to information the solver in the direction of an answer by successively fixing simpler issues that converge to the troublesome drawback.
That is the thought behind utilizing a homotopy technique. We’ll information the solver in the direction of an answer with a easy algorithm that successively provides the solver an excellent heat begin:
Homotopy algorithm
[
begin{aligned}
&textbf{Input:}text{ Initial parameters } varepsilon_{mathrm{ini}}>0, delta_{mathrm{ini}}>0. text{ Tolerances } mathrm{tol}_{varepsilon}>0, mathrm{tol}_{delta}>0.
&textbf{Output:} text{ Solution } (x^{(mathrm{tol}_{varepsilon}, mathrm{tol}_{delta})}, u^{(mathrm{tol}_{varepsilon}, mathrm{tol}_{delta})}) text{ (if it can find one)}
&quad text{Get initial warm start}, (x^{mathrm{warm}}, u^{mathrm{warm}}) text{ (not necessarily feasible)}
&quad i gets 0
&quad textbf{ While } varepsilon > mathrm{tol}_{varepsilon} text{ and } delta > mathrm{tol}_{delta}:
&quadquad varepsilongets max { varepsilon_{mathrm{ini}} / 2^i, mathrm{tol}_{varepsilon} }
&quadquad deltagets max { delta_{mathrm{ini}} / 2^i, mathrm{tol}_{delta} }
& quadquad text{ Solve } NLP_{varepsilon, delta} text{ with warm start } (x^{mathrm{warm}}, u^{mathrm{warm}})
& quadquad text{Label the solution } (x^{(varepsilon, delta)}, u^{(varepsilon, delta)}).
&quadquad (x^{mathrm{warm}}, u^{mathrm{warm}})gets (x^{(varepsilon, delta)}, u^{(varepsilon, delta)}).
&quadquad igets i + 1
&textbf{end while}
&textbf{return}, (x^{(mathrm{tol}_{varepsilon}, mathrm{tol}_{delta})}, u^{(mathrm{tol}_{varepsilon}, mathrm{tol}_{delta})})
end{aligned}
]
NOTE!: The homotopy algorithm is supposed to assist the solver discover a good answer. Nevertheless, there’s no assure that it’s going to efficiently discover even a possible answer, nevermind a globally optimum one. For some concept relating to so-called globallly convergent homotopies you possibly can seek the advice of the papers, [1] and [2].
6. Numerical experiments
On this part we’ll take into account (NLP_{varepsilon, delta}) with preliminary and goal states (x^{mathrm{ini}} = (2,0,frac{pi}{2})) and (x^{mathrm{tar}} = (-2,0,mathrm{free})), respectively (thus (L = 4)). We’ll take the horizon as (T=10) and hold the discretisation step dimension within the RK4 scheme fixed at (h=0.1), thus (Okay=100). Because the management constraints we’ll take (mathbb{U} = [-1,1] instances [-1, 1]), and we’ll take into account this fascinating impediment discipline:

6.1 Checking conditioning
First, we’ll test the issue’s scaling on the heat begin. Stack the state and management into a protracted vector, (mathbf{d}inmbbR^{3K + 2(Okay-1)}), as follows:
[
mathbf{d} := (x_1[0],x_2[0],x_3[0],x_1[1],x_2[1],x_3[1],dots,u_1[0],u_2[0],u_1[1],u_2[1],dots,u_1[K-1],u_2[K-1]),
]
and write (NLP_{varepsilon, delta}) as:
[
newcommand{d}{mathbf{d}}
newcommand{dini}{mathbf{d}^{mathrm{ini}}}
begin{cases}
minlimits_{mathbf{d}} quad & J_{varepsilon,delta}(d)
mathrm{subject to:}
quad & g(d) leq mathbf{0},
end{cases}
]
the place (g) collects all of the constraints. As a heat begin, name this vector (dini), we’ll take the road connecting the preliminary and goal positions, with (u_1[k] equiv 0.1) and (u_2[k] equiv 0).
We must always take a look on the magnitudes of the next portions on the level (dini):
- The price perform, (J_{varepsilon,delta}(dini))
- Its gradient, (nabla J_{varepsilon,delta}(dini))
- Its Hessian, (mathbf{H}(J_{varepsilon,delta}(dini)))
- The constraint residual, (g(dini))
- Its Jacobian, (mathbf{J}(g(dini)))
We are able to do that with the code from the repo:
import numpy as np
from car_OCP import get_initial_warm_start, build_and_check_scaling
x_init = np.array([[2],[0],[np.pi/2]])
x_target = np.array([[-2],[0]])
T = 10 # Horizon size
h = 0.1 # RK4 time step
obstacles = [
{'centre': (0,0), 'radius': 0.5},
{'centre': (-0.5,-0.5), 'radius': 0.2},
{'centre': (1,0.5), 'radius': 0.3},
{'centre': (1,-0.35), 'radius': 0.3},
{'centre': (-1.5,-0.2), 'radius': 0.2},
{'centre': (1.5,-0.2), 'radius': 0.2},
{'centre': (-0.75,0), 'radius': 0.2},
{'centre': (-1.25,0.2), 'radius': 0.2}
]
constraints = {
'u1_min' : -1,
'u1_max' : 1,
'u2_min' : -1,
'u2_max' : 1,
}
warm_start = get_initial_warm_start(x_init, x_target, T, h)
build_and_check_scaling(x_init, x_target, obstacles, constraints, T, h, warm_start, eps=1e-4, delta=1e-4)=== SCALING DIAGNOSTICS ===
Goal J : 1.031e+00
||∇J||_2 : 3.430e-01
||Hess J||_Frob : 1.485e+02
||g||_2 : 7.367e+00
||Jac g||_Frob : 2.896e+01
============================
With small (varepsilon) and (delta), and with our chosen (dini), the target ought to clearly be near 1. The dimensions of its gradient and of the constraint residuals on the heat begin must be of comparable order. Within the print-out, (Vert nabla J Vert_2) denotes the Euclidean norm. The price perform’s Hessian may be of bigger order (this will increase with a finer time step). Within the print-out, (Vert nabla mathrm{Hess} J Vert_{mathrm{Frob}}) is the Frobenius norm of the Hessian matrix, which, intuitively talking, tells you “how massive” the linear transformation is “on common”, so it’s an excellent measure to contemplate. The Jacobian of (g) may also be of barely bigger order.
The print-out reveals that our drawback is well-scaled, nice. However one last item we’ll additionally do is inform IPOPT to scale the issue earlier than we clear up it, with "ipopt.nlp_scaling_method":
.... arrange drawback ....
opts = {"ipopt.print_level": 0,
"print_time": 0,
"ipopt.sb": "sure",
"ipopt.nlp_scaling_method": "gradient-based"}
opti.decrease(price)
opti.solver("ipopt", opts)6.2 Fixing WITHOUT homotopy
This subsection reveals the impact of the parameters (varepsilon) and (delta) on the answer, with out working the homotopy algorithm. In different phrases, we repair (varepsilon) and (delta), and clear up (NLP_{varepsilon, delta}) straight, with out even specifying an excellent preliminary guess. Right here is an instance of how you should utilize the article’s repo to resolve an issue:
import numpy as np
from car_OCP import solve_OCP, get_arc_length, plot_solution_in_statespace_and_control
eps=1e-2
delta=1e-2
x_init = np.array([[2],[0],[np.pi/2]])
x_target = np.array([[-2],[0]])
T = 10 # Horizon size
h = 0.1 # RK4 time step
obstacles = [
{'centre': (0,0), 'radius': 0.5},
{'centre': (-0.5,-0.5), 'radius': 0.2},
{'centre': (1,0.5), 'radius': 0.3},
{'centre': (1,-0.35), 'radius': 0.3},
{'centre': (-1.5,-0.2), 'radius': 0.2},
{'centre': (1.5,-0.2), 'radius': 0.2},
{'centre': (-0.75,0), 'radius': 0.2},
{'centre': (-1.25,0.2), 'radius': 0.2}
]
constraints = {
'u1_min' : -1,
'u1_max' : 1,
'u2_min' : -1,
'u2_max' : 1,
}
x_opt, u_opt = solve_OCP(x_init, x_target, obstacles, constraints, T, h, warm_start=None, eps=eps, delta=delta)
plot_solution_in_statespace_and_control(x_opt, u_opt, obstacles, arc_length=np.spherical(get_arc_length(x_opt), 2), obstacles_only=False, eps=eps, delta=delta)Word how the solver may discover regionally optimum options which are clearly not so good, like within the case (varepsilon) = (delta) = 1e-4. That is one motivation for utilizing homotopy: you can information the solver to a greater regionally optimum answer. Word how (delta) impacts the chattering, with it being actually unhealthy when (delta=0). The solver simply fails when (varepsilon=0).



6.3 Fixing WITH homotopy
Let’s now clear up the issue with the homotopy algorithm. I.e., we iterate over (i) and feed the solver the earlier drawback’s answer as a heat begin on every iteration. The preliminary guess we offer (at (i=0)) is identical one we used once we checked the conditioning, that’s, it’s simply the road connecting the preliminary and goal positions, with (u_1[k] equiv 0.1) and (u_2[k] equiv 0).
The figures under present the answer obtained at numerous steps of the iteration within the homotopy algorithm. The parameter (delta) is saved above 1e-4, so we don’t have chattering.



As one would anticipate, the arc size of the answer obtained through the homotopy algorithm monotonically decreases with growing (i). Right here, (delta)=1e-4 all through.

7. Conclusion
I’ve thought of a troublesome optimum management drawback and gone by the steps one must comply with to resolve it intimately. I’ve proven how one can virtually take care of problems with nondifferentiability and management chattering, and the way a easy homotopy technique can result in options of larger high quality.
8. Additional studying
A basic e-book on sensible points surrounding optimum management is [3]. Seek the advice of the papers [4] and [5] for well-cited surveys of numerical strategies in optimum management. The e-book [6] is one other glorious reference on numerical strategies.
References
[1] Watson, Layne T. 2001. “Idea of Globally Convergent Likelihood-One Homotopies for Nonlinear Programming.” SIAM Journal on Optimization 11 (3): 761–80. https://doi.org/10.1137/S105262349936121X.
[2] Esterhuizen, Willem, Kathrin Flaßkamp, Matthias Hoffmann, and Karl Worthmann. 2025. “Globally Convergent Homotopies for Discrete-Time Optimum Management.” SIAM Journal on Management and Optimization 63 (4): 2686–2711. https://doi.org/10.1137/23M1579224.
[3] Bryson, Arthur Earl, and Yu-Chi Ho. 1975. Utilized Optimum Management: Optimization, Estimation and Management. Taylor; Francis.
[4] Betts, John T. 1998. “Survey of Numerical Strategies for Trajectory Optimization.” Journal of Steering, Management, and Dynamics 21 (2): 193–207.
[5] Rao, Anil V. 2009. “A Survey of Numerical Strategies for Optimum Management.” Advances within the Astronautical Sciences 135 (1): 497–528.
[6] Gerdts, Matthias. 2023. Optimum Management of ODEs and DAEs. Walter de Gruyter GmbH & Co KG.