Non-Parametric Density Estimation: Theory and Applications

In , we’ll discuss what Density Estimation is and the position it performs in statistical evaluation. We’ll analyze two common density estimation strategies, histograms and kernel density estimators, and analyze their theoretical properties in addition to how they carry out in observe. Lastly, we’ll take a look at how density estimation could also be used as a software for classification duties. Hopefully after studying this text, you allow with an appreciation of density estimation as a elementary statistical software, and a strong instinct behind the density estimation approaches we focus on right here. Ideally, this text may even spark an curiosity in studying extra about density estimation and level you in direction of further assets that will help you dive deeper than what’s mentioned right here!

Contents:

---

Background Ideas

Studying/refreshing on the next ideas will likely be useful to completely admire the remainder of what’s mentioned on this article.

---

What’s density estimation?

Density estimation is anxious with reconstructing the chance density operate of a random variable, X, given a pattern of random variates X₁, X₂,…, X_n.

Density estimation performs a vital position in statistical evaluation. It might be used as a standalone technique for analyzing the properties of a random variable’s distribution, resembling modality, unfold, and skew. Alternatively, density estimation could also be used as a method for additional statistical evaluation, resembling classification duties, goodness-of-fit assessments, and anomaly detection, to call a couple of.

A few of chances are you’ll recall that the chance distribution of a random variable X may be fully characterised by its cumulative distribution operate (CDF), F(⋅).

• If X is a discrete random variable, then we will derive its chance mass operate (PMF), p(⋅), from its CDF through the next relationship: p(X_i) = F(X_i) − F(X_i-1), the place X_i-1 denotes the most important worth throughout the discrete distribution of X that’s lower than X_i.
• If X is steady, then its chance density operate (PDF), p(⋅), could also be derived by differentiating its CDF i.e. F′(⋅) = p(⋅).

Primarily based on this, chances are you’ll be questioning why we’d like strategies to estimate the chance distribution of X, after we can simply exploit the relationships said above.

Definitely, given a pattern of knowledge X₁,…, X_n, we could at all times assemble an estimate of its CDF. If X is discrete, then developing its PMF is easy, because it merely requires counting the frequency of observations for every distinct worth that seems in our pattern.

Nevertheless, if X is steady, estimating its PDF shouldn’t be so trivial. Discover that our estimate of the CDF, F(⋅), will essentially comply with a discrete distribution, since we’ve a finite quantity of empirical knowledge. Since F(⋅) is discrete, we can’t merely differentiate it to acquire an estimate of the PDF. Thus, this motivates the necessity for different strategies of estimating p(⋅).

To supply some further motivation behind density estimation, the CDF could also be suboptimal to make use of for analyzing the properties of the chance distribution of X. For instance, take into account the next show.

Sure properties of the distribution of X, resembling its bimodal nature, are instantly clear from analyzing its PDF. Nevertheless, these properties are more durable to note from analyzing its CDF, because of the cumulative nature of the distribution. For a lot of people, the PDF seemingly offers a extra intuitive show of the distribution of X — it’s bigger at values of X which might be extra prone to “happen” and smaller for values of X which might be much less seemingly.

Broadly talking, density estimation approaches could also be categorized as parametric or non-parametric.

• Parametric density estimation assumes X follows some distribution that could be characterised by some parameters (ex: X ∼ N(μ,σ)). Density estimation on this case includes estimating the related parameters for the parametric distribution of X, after which plugging in these parameter estimates to the corresponding density operate formulation for X.
• Non-parametric density estimation makes much less inflexible assumptions in regards to the distribution of X, and estimates the form of the density operate instantly from the empirical knowledge. In consequence, non-parametric density estimates will usually have decrease bias and better variance in comparison with parametric density estimates. Non-parametric strategies could also be desired when the underlying distribution of X is unknown and we’re working with a considerable amount of empirical knowledge.

For the remainder of this text, we’ll concentrate on analyzing two common non-parametric strategies for density estimation: Histograms and kernel density estimators (KDEs). We’ll dig into how they work, the advantages and disadvantages of every strategy, and the way precisely they estimate the true density operate of a random variable. Lastly, we’ll study how density estimation may be utilized to classification issues, and the way the standard of the density estimator can impression classification efficiency.

---

Histograms

Overview

Histograms are a easy non-parametric strategy for developing a density estimate from a pattern of knowledge. Intuitively, this strategy includes partitioning the vary of our knowledge into distinct equal size bins. Then, for any given level, assign its density to be equal to the proportion of factors that reside throughout the identical bin, normalized by the bin size.

Formally, given a pattern of n observations

partition the area into M bins

such that

For a given level x ∈ β_l, the place β_l denotes the lth bin, the density estimate produced by the histogram will likely be

For the reason that histogram density estimator assigns uniform density to all factors throughout the identical bin, the density estimate will likely be discontinuous in any respect of its breakpoints the place the density estimates differ.

Above, we’ve the histogram density estimate of the usual Gaussian distribution generated from a pattern of 1000 knowledge factors. We see that x = 0 and x = −0.5 lie throughout the identical bin, and thus have equivalent density estimates.

Theoretical Properties

Histograms are a easy and intuitive technique for density estimation. They make no assumptions in regards to the underlying distribution of the random variable. Histogram estimation merely requires tuning the bin width, h, and the purpose the place the histogram bins originate from, t₀. Nevertheless, we’ll see very quickly that the accuracy of the histogram estimator is very depending on tuning these parameters appropriately.

As desired, the histogram estimator is a real density operate.

• It’s non-negative over its complete area.
• It integrates to 1.

We will consider the accuracy of the histogram estimator for estimating the true density, p(⋅), by decomposing its imply squared error into its bias and variance phrases.

First, lets study its bias at a given level x ∈ (b_k-1, b_ok].

Let’s take a little bit of a leap right here. Utilizing the Taylor collection enlargement, the truth that the PDF is the spinoff of the CDF, and |x − b_k-1| ≤ h, we will derive the next.

Thus, we’ve

which means

Subsequently, the histogram estimator is an unbiased estimator of the true density, p(⋅), because the bin width approaches 0.

Now, let’s analyze the variance of the histogram estimator.

Discover that as h → ∞, we’ve

Subsequently,

Now, we’re at a little bit of an deadlock; we see that as h → ∞, the bias of the histogram density estimate decreases, whereas its variance will increase. 

We’re usually involved with the accuracy of the density estimate at massive pattern sizes (i.e. as n → ∞). Subsequently, to maximise the accuracy of the histogram density estimate, we’ll need to tune h to realize the next conduct:

• Select h to be small to attenuate bias.
• As h → 0 and n → ∞, we should have nh → ∞ to attenuate variance. In different phrases, the big pattern dimension ought to overpower the small bin width, asymptotically.

This bias-variance trade-off shouldn’t be sudden:

• Small bin widths could seize the density round a selected level with excessive precision. Nevertheless, density estimates could change from small random variations throughout knowledge units as much less factors will fall throughout the identical bin.
• Massive bin widths embody extra knowledge factors when computing the density estimate at a given level, which implies density estimates will likely be extra strong to small random variations within the knowledge.

Let’s illustrate this trade-off with some examples.

Demonstration of Theoretical Properties

First, we’ll take a look at how small bin widths could result in massive variance within the histogram density estimator. For this instance, we’ll draw 4 samples of fifty random variates, the place every pattern is drawn from an ordinary Gaussian distribution. We’ll set a comparatively small bin width (h = 0.2).

set.seed(25)

# Customary Gaussian
mu <- 0
sd <- 1

# Parameters for density estimate
n <- 50
h <- 0.2

# Generate 4 samples of ordinary Gaussian
samples <- replicate(4, rnorm(n, imply = mu, sd = sd), simplify = FALSE)

# Setup 2x2 plot
par(mfrow = c(2, 2), mar = c(4, 4, 3, 1))

# Plot histograms
titles <- paste("Pattern", 1:4)
invisible(mapply(plot_histogram, samples, title = titles,
       MoreArgs = record(binwidth = h, origin = 0, line = 0)))

It’s clear that the histogram density estimates differ fairly a bit. As an illustration, we see that the pointwise density estimate at x = 0 ranges from roughly 0.2 in Pattern 4 to roughly 0.6 in Pattern 2. Moreover, the distribution of the density estimate produced in Pattern 1 seems virtually bimodal, with peaks round −1 and a bit above 0.

Let’s repeat this train to exhibit how massive bin widths could lead to a density estimate with decrease variance, however greater bias. For this instance, let’s draw 4 samples from a bimodal distribution consisting of a mix of two Gaussian distributions, N(0, 1) and N(3, 1). We’ll set a comparatively massive bin width (h = 2).

set.seed(25)

# Bimodal distribution parameters - combination of N(0, 1) and N(4, 1)
mu_1 <- 0
sd_1 <- 1
mu_2 <- 3
sd_2 <- 1

# Density estimation parameters
n <- 100
h <- 2

# Generate 4 samples from bimodal distribution
samples <- replicate(4, c(rnorm(n/2, imply = mu_1, sd = sd_1), rnorm(n/2, imply = mu_2, sd = sd_2)), simplify = FALSE)

# Arrange 2x2 plotting grid
par(mfrow = c(2, 2), mar = c(4, 4, 3, 1))

# Plot histograms
titles <- paste("Pattern", 1:4)
invisible(mapply(plot_histogram, samples, title = titles,
       MoreArgs = record(binwidth = h, origin = 0, line = 0)))

There’s nonetheless some variation within the density estimates throughout the 4 histograms, however they seem steady relative to the density estimates we noticed above with smaller bin widths. As an illustration, it seems that the pointwise density estimate at x = 0 is roughly 0.15 throughout all of the histograms. Nevertheless, it’s clear that these histogram estimators introduce a considerable amount of bias, because the bimodal distribution of the true density operate is masked by the big bin widths.

Moreover, we talked about beforehand that the histogram estimator requires tuning the origin level, t₀. Let’s take a look at an instance that illustrates the impression that the selection of t₀ can have on the histogram density estimate.

set.seed(123)

# Distribution and density estimation parameters
# Bimodal distribution: combination of N(0, 1) and N(5, 1)
n <- 50
knowledge <- c(rnorm(n/2, imply = 0, sd = 1), rnorm(n/2, imply = 5, sd = 1))
h <- 3

# Arrange plotting grid
par(mfrow = c(1, 2), mar = c(4, 4, 3, 1))

# Identical bin width, totally different origins
plot_histogram(knowledge, binwidth = h, origin = 0, title = paste("Bin width = ", h, ", Origin = 0"))
plot_histogram(knowledge, binwidth = h, origin = 1, title = paste("Bin width = ", h, ", Origin = 1"))

The histogram density estimates above differ of their origin level by a magnitude of 1. The impression of the totally different origin level on the ensuing histogram density estimates is clear. The histogram on the left captures the truth that the distribution is bimodal with peaks round 0 and 5. In distinction, the histogram on the suitable gives the look that the density of X follows a unimodal distribution with a single peak round 5.

Histograms are a easy and intuitive strategy to density estimation. Nevertheless, histograms will at all times produce density estimates that comply with a discrete distribution, and we’ve seen that the ensuing density estimate could also be extremely depending on an arbitrary alternative of the origin level. Subsequent, we’ll take a look at another technique for density estimation, Kernel Density Estimation, that addresses these shortcomings.

---

Kernel Density Estimators (KDE)

Naive Density Estimator

We’ll first take a look at probably the most fundamental type of a kernel density estimator, the naive density estimator. This strategy is often known as the “transferring histogram”; it’s an extension of the normal histogram density estimator that computes the density at a given level by inspecting the variety of observations that fall inside an interval that’s centered round that time.

Formally, the pointwise density estimate at x produced by the naive density estimator may be written as follows.

Its corresponding kernel is outlined as follows.

Not like the normal histogram density estimate, the density estimate produced by the transferring histogram doesn’t differ based mostly on the selection of origin level. In reality, there is no such thing as a idea of “origin level” within the transferring histogram, because the density estimate at x solely will depend on the factors that lie throughout the neighborhood (x − (h/2), x + (h/2)).

Let’s study the density estimate produced by the naive density estimator for a similar bimodal distribution as we used above for highlighting the histogram’s dependency on origin level.

set.seed(123)

# Bimodal distribution - combination of N(0, 1) and N(5, 1)
knowledge <- c(rnorm(n/2, imply = 0, sd = 1), rnorm(n/2, imply = 5, sd = 1))

# Density estimate parameters
n <- 50
h <- 1 

# Naive Density Estimator: KDE with rectangular kernel utilizing half the bin width
# Rectangular kernel counts factors inside (x - h, x + h)
pdf_est <- density(knowledge, kernel = "rectangular", bw = h/2) 

# Plot PDF
plot(pdf_est, fundamental = "NDE: Bimodal Gaussian", xlab = "x", ylab = "Density", col = "blue", lwd = 2)
rug(knowledge)
polygon(pdf_est, col = rgb(0, 0, 1, 0.2), border = NA)
grid()

Clearly, the density estimate produced by the naive density estimator captures the bimodal distribution far more precisely than the normal histogram. Moreover, the density at every level is captured with a lot finer granularity.

That being stated, the density estimate produced by the NDE continues to be fairly “tough” i.e. the density estimate doesn’t have easy curvature. It is because every remark is weighted as “all or nothing” when computing the pointwise density estimate, which is apprent from its kernel, Okay₀. Particularly, all factors throughout the neighborhood (x − (h/2), x + (h/2)) contribute equally to the density estimate, whereas factors exterior the interval contribute nothing.

Ideally, when computing the density estimate for x, we wish to weigh factors in proportion to their distance from x, such that the factors nearer/farther from x have the next/decrease impression on its density estimate, respectively.

That is primarily what the KDE does: it generalizes the naive density estimator by changing the uniform density operate with an arbitrary density operate, the kernel. Intuitively, you may consider the KDE as a smoothed histogram.

KDE: Overview

The kernel density estimator generated from a pattern X₁,…, X_n, may be outlined as follows:

Beneath are some common decisions for kernels utilized in density estimation.

These are simply a number of of the extra common kernels which might be usually used for density estimation. For extra details about kernel features, take a look at the Wikipedia. In the event you’re in search of for some instinct behind what precisely a kernel operate is (as I used to be), take a look at this quora thread.

We will see that the KDE is a real density operate.

• It’s at all times non-negative, since Okay(⋅) is a density operate.
• It integrates to 1.

Kernel and Bandwidth

In observe, Okay(⋅) is chosen to be symmetric and unimodal round 0 (∫u⋅Okay(u)du = 0). Moreover, Okay(⋅) is often scaled to have unit variance when used for density estimation (∫u²⋅Okay(u)du = 1). This scaling primarily standardizes the impression that the selection of bandwidth, h, has on the KDE, whatever the kernel getting used.

For the reason that KDE at a given level is the weighted sum of its neighboring factors, the place the weights are computed by Okay(⋅), the smoothness of the density estimate is inherited from the smoothness of the kernel operate.

• Clean kernel features will produce easy KDEs. We will see that the Gaussian kernel depicted above is infinitely differentiable, so KDEs with the Gaussian kernel will produce density estimates with easy curvature.
• However, the opposite kernel features (Epanechnikov, rectangular, triangular) will not be differentiable in every single place (ex: ±1), and within the case of the oblong and triangular kernels, should not have easy curvature. Thus, KDEs utilizing these kernels will produce rougher density estimates.

Nevertheless, in observe, we’ll see that so long as the kernel operate is steady, the selection of the kernel has comparatively little impression on the KDE in comparison with the selection of bandwidth.

set.seed(123)

# pattern from normal Gaussian
x <- rnorm(50)

# kernel/bandwidths for KDEs
kernels <- c("gaussian", "epanechnikov", "rectangular", "triangular")
bandwidths <- c(0.5, 1, 2)

colors_k <- rainbow(size(kernels))
colors_b <- rainbow(size(bandwidths))

plot_kde_comparison <- operate(values, label, sort = c("kernel", "bandwidth")) {
  sort <- match.arg(sort)
  plot(NULL, xlim = vary(x) + c(-1, 1), ylim = c(0, 0.5),
       xlab = "x", ylab = "Density", fundamental = paste("KDE with Totally different", label))

  for (i in seq_along(values)) {
    if (sort == "kernel") {
      d <- density(x, kernel = values[i])
      col <- colors_k[i]
    } else {
      d <- density(x, bw = values[i], kernel = "gaussian")
      col <- colors_b[i]
    }
    strains(d$x, d$y, col = col, lwd = 2)
  }

  curve(dnorm(x), add = TRUE, lty = 2, lwd = 2)
  legend("topright", legend = c(as.character(values), "True Density"),
         col = c(if (sort == "kernel") colors_k else colors_b, "black"),
         lwd = 2, lty = c(rep(1, size(values)), 2), cex = 0.8)
  rug(x)
}

plot_kde_comparison(kernels, "Kernels", sort = "kernel")
plot_kde_comparison(bandwidths, "Bandwidths", sort = "bandwidth")

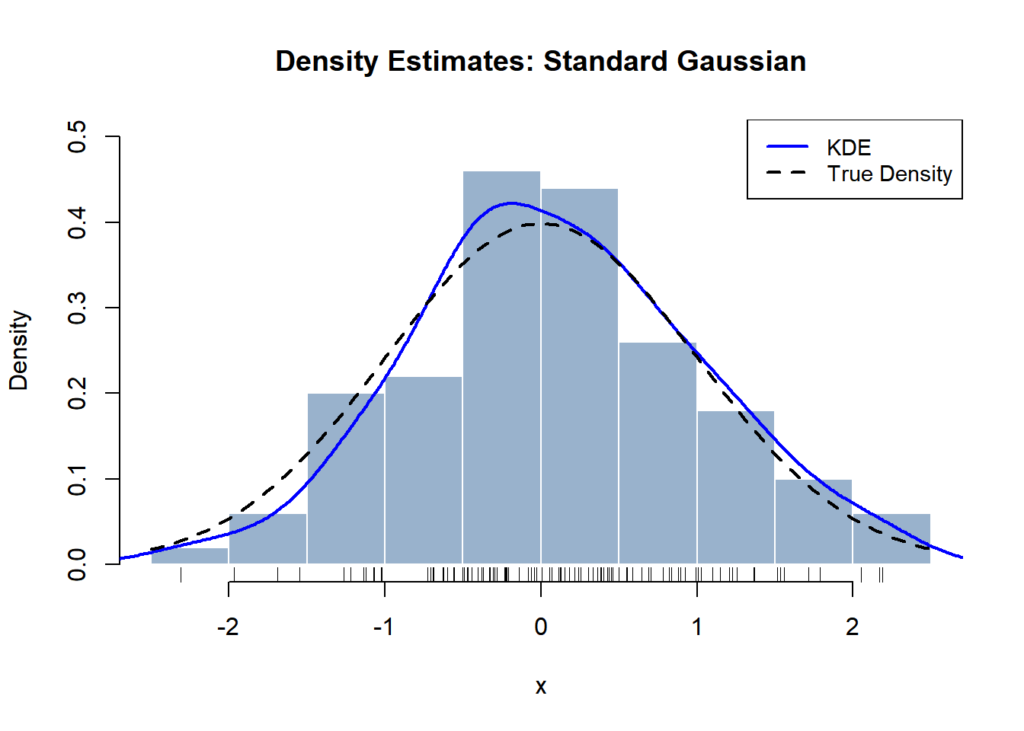
We see that the KDEs for the usual Gaussian with varied kernels are comparatively related, in comparison with the KDEs produced with varied bandwidths.

Accuracy of the KDE

Let’s study how precisely the KDE estimates the true density, p(⋅). As we did with the histogram estimator, we will decompose its imply squared error into its bias and variance phrases. For particulars behind the way to derive these bias and variance phrases, take a look at lecture 6 of these notes.

The bias and variance of the KDE at x may be expressed as follows.

Intuitively, these outcomes give us the next insights:

• The impact of Okay(⋅) on the accuracy of the KDE is primarily captured through the time period σ²_Okay = ∫Okay(u)²du. The Epanechnikov kernel minimizes this integral, so theoretically it ought to produce the optimum KDE. Nevertheless, we’ve seen that the selection of kernel has little sensible impression on the KDE relative to its bandwidth. Moreover, the Epanechnikov kernel has a bounded help interval ([−1, 1]). In consequence, it might produce rougher density estimates relative to kernels which might be nonzero throughout your entire actual quantity house (ex: Gaussian). Thus, the Gaussian kernel is often utilized in observe.
• Recall that the asymptotic bias and variance of the histogram estimator as h → ∞ was O(h) and O(1/(nh)), respectively. Evaluating these towards KDE tells us that the KDE improves upon the histogram density estimator primarily by means of decreased asymptotic bias. That is anticipated: the kernel easily varies the burden of the neighboring factors of x when computing the pointwise density at x, as an alternative of assigning uniform density to arbitrary mounted intervals of the area. In different phrases, the KDE imposes a much less inflexible construction on the density estimate in comparison with the histogram strategy.

For histograms and KDEs, we’ve seen that the bandwidth h can have a major impression on the accuracy of the density estimate. Ideally, we would choose the h such that the imply squared error of the density estimator is minimized. Nevertheless, it seems that this theoretically optimum h will depend on the curvature of the true density p(⋅), which is unknown observe (in any other case we wouldn’t want density estimation)!

Some common approaches for bandwidth choice embody:

• Assuming the true density resembles some reference distribution p₀(⋅) (ex: Gaussian), then plugging within the curvature of p₀(⋅) to derive the bandwidth. This approach is easy, but it surely assumes the distribution of the info, so it might be a poor alternative if you happen to’re seeking to construct density estimates to discover your knowledge.
• Non-parametric approaches to bandwidth choice, resembling cross-validation and plug-in strategies. The unbiased cross-validation and Sheather-Jones strategies are common bandwidth selectors and usually produce pretty correct density estimates.

For extra info on the impression of bandwidth choice on the KDE, take a look at this blog post.

set.seed(42)

# Simulate knowledge: a bimodal distribution
x <- c(rnorm(150, imply = -2), rnorm(150, imply = 2))

# Outline true density
true_density <- operate(x) {
  0.5 * dnorm(x, imply = -2, sd = 1) + 
  0.5 * dnorm(x, imply = 2, sd = 1)
}

# Create plotting vary
x_grid <- seq(min(x) - 1, max(x) + 1, size.out = 500)
xlim <- vary(x_grid)
ylim <- c(0, max(true_density(x_grid)) * 1.2)

# Base plot
plot(NULL, xlim = xlim, ylim = ylim,
     fundamental = "KDE: Varied Bandwidth Choice Strategies",
     xlab = "x", ylab = "Density")

# KDE with totally different bandwidths
strains(density(x), col = "crimson", lwd = 2, lty = 4)
h_scott <- 1.06 * sd(x) * size(x)^(-1/5)
strains(density(x, bw = h_scott), col = "blue", lwd = 2, lty = 2)
strains(density(x, bw = bw.ucv(x)), col = "darkgreen", lwd = 2, lty = 3)
strains(density(x, bw = bw.SJ(x)), col = "purple", lwd = 2, lty = 4)

# True density
strains(x_grid, true_density(x_grid), col = "black", lwd = 2)

# Add legend
legend("topright",
       legend = c("Silverman (Default))", "Scott's Rule", "Unbiased CV",
                  "Sheather-Jones", "True Density"),
       col = c("crimson", "blue", "darkgreen", "purple", "black"),
       lty = 1:6, lwd = 2, cex = 0.8)

---

Density Estimation for Classification

We’ve mentioned an awesome deal in regards to the underlying principle of histograms and KDE, and we’ve demonstrated how they carry out at modeling the true density of some pattern knowledge. Now, we’ll take a look at how we will apply what we realized about density estimation for a easy classification process.

As an illustration, say we need to construct a classifier from a pattern of n observations (x₁, y₁),…, (x_n, y_n), the place every x_i comes from a p-dimensional function house, X, and y_i corresponds to the goal labels drawn from Y = {1,…, m}.

Intuitively, we need to construct a classifier such that for every remark, our classifier assigns it the category label ok such that the next is glad.

The Bayes classifier does exactly that, and computes the conditional chance above utilizing the next equation.

This classifier depends on the next:

• π_ok = P(Y = ok): the prior chance that an remark (x_i, y_i) belongs to the okth class (i.e. y_i = ok). This may be estimated by merely counting the proportion of factors in every class from our pattern knowledge.
• f_ok(x) ≡ P(X = x | Y = ok): the p-dimensional density operate of X for all observations in goal class ok. That is more durable to estimate: for every of the m goal courses, we should decide the form of the distribution for every dimension of X, and in addition whether or not there are any associations between the totally different dimensions.

The Bayes classifier is optimum if the portions above may be computed exactly. Nevertheless, that is inconceivable to realize in observe when working with a finite pattern of knowledge. For extra element behind why the Bayes classifier is perfect, take a look at this site.

So the query turns into, how can we approximate the Bayes classifier?

One common technique is the Naive Bayes classifier. Naive Bayes assumes class-conditional independence, which implies that for every goal class, it reduces the p-dimensional density estimation downside into p separate univariate density estimation duties. These univariate densities could also be estimated parametrically or non-parametrically. A typical parametric strategy would assume that every dimension of X follows a univariate Gaussian distribution with class-specific imply and a diagonal co-variance matrix, whereas a non-parametric strategy could mannequin every dimension of X utilizing a histogram or KDE.

The parametric strategy to univariate density estimation in Naive Bayes could also be helpful when we’ve a small quantity of knowledge relative to the scale of the function house, because the bias launched by the Gaussian assumption could assist scale back the variance of the classifier. Nevertheless, the Gaussian assumption could not at all times be applicable relying on the distribution of knowledge that you simply’re working with.

Let’s study how parametric vs. non-parametric density estimates can impression the choice boundary of the Naive Bayes classifier. We’ll construct two classifiers on the Iris dataset: one in every of them will assume every function follows a Gaussian distribution, and the opposite will construct kernel density estimates for every function.

# Parametric Naive Bayes
param_nb <- naive_bayes(Species ~ ., knowledge = prepare)

# Nonparametric Naive Bayes
# KDE with Gaussian kernel and Sheather-Jones bandwidth
nonparam_nb <- naive_bayes(Species ~ ., knowledge = prepare, 
                           usekernel = TRUE, 
                           kernel="gaussian",
                           bw="sj") # play with bandwidth to see the way it impacts the classification boundaries!

# Create grid for plotting determination boundaries
x_seq <- seq(min(iris2D$Sepal.Size), max(iris2D$Sepal.Size), size.out = 200)
y_seq <- seq(min(iris2D$Petal.Size), max(iris2D$Petal.Size), size.out = 200)
grid <- increase.grid(Sepal.Size = x_seq, Petal.Size = y_seq)

# Predict class for every level on grid
grid$param_pred <- predict(param_nb, grid)
grid$nonparam_pred <- predict(nonparam_nb, grid)

# Plot determination boundaries
nb_parametric <- ggplot() +
  geom_tile(knowledge = grid, aes(x = Sepal.Size, y = Petal.Size, fill = param_pred), alpha = 0.3) +
  geom_point(knowledge = prepare, aes(x = Sepal.Size, y = Petal.Size, shade = Species), dimension = 2) +
  ggtitle("Parametric Naive Bayes Choice Boundary") +
  theme_minimal()

nb_nonparametric <- ggplot() +
  geom_tile(knowledge = grid, aes(x = Sepal.Size, y = Petal.Size, fill = nonparam_pred), alpha = 0.3) +
  geom_point(knowledge = prepare, aes(x = Sepal.Size, y = Petal.Size, shade = Species), dimension = 2) +
  ggtitle("Nonparametric Naive Bayes Choice Boundary") +
  theme_minimal()

nb_parametric
nb_nonparametric

# Parametric Naive Bayes prediction on check knowledge
param_pred <- predict(param_nb, newdata = check)

# Non-parametric Naive Bayes prediction on check knowledge
nonparam_pred <- predict(nonparam_nb, newdata = check)

# Create confusion matrices
param_cm <- confusionMatrix(param_pred, check$Species)
nonparam_cm <- confusionMatrix(nonparam_pred, check$Species)

output <- seize.output({
  # Print confusion matrices
  cat("n=== Parametric Naive Bayes Metrics ===n")
  print(param_cm$desk)
  cat("Parametric Naive Bayes Accuracy: ", param_cm$total['Accuracy'], "nn")
  
  cat("=== Non-parametric Naive Bayes Metrics ===n")
  print(nonparam_cm$desk)
  cat("Nonparametric Naive Bayes Accuracy: ", nonparam_cm$total['Accuracy'], "n")
})
cat(paste(output, collapse = "n"))

We see that the non-parametric Naive Bayes classifier achieves barely higher accuracy than its parametric counterpart. It is because the non-parametric density estimates produce a classifier with a extra versatile determination boundary. In consequence, a number of of the “virginica” observations that have been incorrectly categorised as “versicolor” by the parametric classifier ended up being categorised accurately by the non-parametric mannequin.

That being stated, the choice boundaries produced by non-parametric Naive Bayes look like tough and disconnected. Thus, there are some areas of the function house the place the classification boundary could also be questionable, and fail to generalize effectively to new knowledge. In distinction, the parametric Naive Bayes classifier produces easy, linked determination boundaries that seem to precisely seize the overall sample of the function distributions for every species.

This distinction brings up an necessary level that “extra versatile density estimation” doesn’t equate to “higher density estimation”, particularly when utilized to classification. In any case, there’s a motive why Naive Bayes classification is common. Though making much less assumptions in regards to the distribution of your knowledge could seem fascinating to supply unbiased density estimates, simplifying assumptions could also be efficient when there’s inadequate empirical knowledge to supply top quality estimates, or if the parametric assumptions are believed to be principally correct. Within the latter case, parametric estimation will introduce little to no bias to the estimator, whereas non-parametric approaches could introduce massive quantities of variance.

Certainly, wanting on the function distributions under, the Gaussian assumption of parametric Naive Bayes doesn’t appear inappropriate. For probably the most half, it seems the category distributions for petal and sepal size look like unimodal and symmetric.

iris_long <- pivot_longer(iris, cols = c(Sepal.Size, Petal.Size), names_to = "Function", values_to = "Worth")

ggplot(iris_long, aes(x = Worth, fill = Species)) +
  geom_density(alpha = 0.5, bw="sj") +
  facet_wrap(~ Function, scales = "free") +
  labs(title = "Distribution of Sepal and Petal Lengths by Species", x = "Size (cm)", y = "Density") +
  theme_minimal()

---

Wrap-up

Thanks for studying! We dove into the idea behind the histogram and kernel density estimators and the way to apply them in context..

Let’s briefly summarize what we mentioned:

• Density estimation is a elementary software in Statistical Analysis for analyzing the distribution of a variable or as an intermediate software for deeper statistical evaluation. Density estimation approaches could also be broadly categorized as parametric or non-parametric.
• Histograms and KDEs are two common approaches for non-parametric density estimation. Histograms produce density estimates by computing the normalized frequency of factors inside every distinct bin of the info. KDEs are “smoothed” histograms that estimate the density at a given level by computing a weighted sum of its surrounding factors, the place neighbors are weighted in proportion to their distance.
• Non-parametric density estimation may be utilized to classification algorithms that require modeling the function densities for every goal class (Bayesian classification). Classifiers constructed utilizing non-parametric density estimates could possibly outline extra versatile determination boundaries at the price of greater variance.

Try the sources under if you happen to’re fascinated by studying extra!

The creator has created all pictures on this article.

---

Sources

Studying Sources:

Datasets:

• Fisher, R. (1936). Iris [Dataset]. UCI Machine Studying Repository. https://doi.org/10.24432/C56C76. (CC BY 4.0)