knowledge analytics for a yr now. Thus far, I can contemplate myself assured in SQL and Energy BI. The transition to Python has been fairly thrilling. I’ve been uncovered to some neat and smarter approaches to knowledge evaluation.
After brushing up on my expertise on the Python fundamentals, the best subsequent step was to start out studying about among the Python libraries for knowledge evaluation. NumPy is one among them. Being a math nerd, naturally, I’d take pleasure in exploring this Python library.
This library is designed for people who need to carry out mathematical computations utilizing Python, from primary arithmetic and algebra to superior ideas like calculus. NumPy can just about do all of it.
On this article, I needed to introduce you to some NumPy features I’ve been enjoying round with. Whether or not you’re a knowledge scientist, monetary analyst, or analysis nerd, these features would enable you out lots. With out additional ado, let’s get to it.
Pattern Dataset (used all through)
Earlier than diving in, I’ll outline a small dataset that may anchor all examples:
import numpy as np
temps = np.array([30, 32, 29, 35, 36, 33, 31])Utilizing this small temperature dataset, I’ll be sharing 7 features that make array operations easy.
1. np.the place()— The Vectorized If-Else
Earlier than I outline what this operate is, right here’s a fast showcase of the operate
arr = np.array([10, 15, 20, 25, 30])
indices = np.the place(arr > 20)
print(indices)Output: (array([3, 4]),)
np.the place is a condition-based operate. When a situation is specified, it outputs the index/indices the place that situation is true.
For example, within the instance above, an array is specified, and I’ve declared a np.the place operate that retrieves information the place the array aspect is bigger than 20. The output is array([3, 4]), as a result of that’s the situation/indices the place that situation is true — that might be 25 and 30.
Conditional choice/alternative
It’s additionally helpful once you’re making an attempt to outline a customized output for the outputs that meet your situation. That is used lots in knowledge evaluation. For example:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
outcome = np.the place(arr % 2 == 0, ‘even’, ‘odd’)
print(outcome)Output: [‘odd’ ‘even’ ‘odd’ ‘even’ ‘odd’]
The instance above tries to retrieve even numbers. After retrieving, a situation choice/alternative operate is known as that provides a customized title to our circumstances. If the situation is true, it’s changed by even, and if the situation is fake, it’s changed by odd.
Alright, let’s apply this to our small dataset.
Drawback: Change all temperatures above 35°C with 35 (cap excessive readings).
In real-world knowledge, particularly from sensors, climate stations, or person inputs, outliers are fairly widespread — sudden spikes or unrealistic values that aren’t reasonable.
For instance, a temperature sensor may momentarily glitch and document 42°C when the precise temperature was 35°C.
Leaving such anomalies in your knowledge can:
- Skew averages — a single excessive worth can pull your imply upward.
- Distorted visualisations — charts may stretch to accommodate a number of excessive factors.
- Mislead fashions — machine studying algorithms are delicate to surprising ranges.
Let’s repair that
adjusted = np.the place(temps > 35, 35, temps)Output: array([30, 32, 29, 35, 35, 33, 31])
Appears significantly better now. With only a few traces of code, we managed to repair unrealistic outliers in our dataset.
2. np.clip() — Maintain Values in Vary
In lots of sensible datasets, values can spill outdoors the anticipated vary, in all probability as a result of measurement noise, person error, or scaling mismatches.
For example:
- A temperature sensor may learn −10°C when the bottom doable is 0°C.
- A mannequin output may predict chances like 1.03 or −0.05 as a result of rounding.
- When normalising pixel values for a picture, a number of may transcend 0–255.
These “out-of-bounds” values could appear minor, however they will:
- Break downstream calculations (e.g., log or proportion computations).
- Trigger unrealistic plots or artefacts (particularly in sign/picture processing).
- Distort normalisation and make metrics unreliable.
np.clip() neatly solves this downside by constraining all components of an array inside a specified minimal and most vary. It’s kinda like setting boundaries in your dataset.
Instance:
Drawback: Guarantee all readings keep inside [28, 35] vary.
clipped = np.clip(temps, 28, 35)
clippedOutput: array([30, 32, 29, 35, 35, 33, 31])
Right here’s what it does:
- Any worth under 28 turns into 28.
- Any worth above 35 turns into 35.
- The whole lot else stays the identical.
Positive, this is also achieved with np.the place() like sotemps = np.the place(temps < 28, 28, np.the place(temps > 35, 35, temps))
However I’d slightly go together with np.clip() cos it’s a lot cleaner and sooner.
3. np.ptp() — Discover Your Information’s Vary in One Line
np.ptp() (peak-to-peak) mainly exhibits you the distinction between the utmost and minimal components.
It’s mainly:np.ptp(a) == np.max(a) — np.min(a)
However in a single clear, expressive operate.
Right here’s the way it works
arr = np.array([[1, 5, 2],
[8, 3, 7]])
# Calculate peak-to-peak vary of your entire array
range_all = np.ptp(arr)
print(f”Peak-to-peak vary of your entire array: {range_all}”)In order that’ll be our most worth (8) — minimal worth(1)
Output: Peak-to-peak vary of your entire array: 7
So why is this convenient? Just like averages, understanding how a lot your knowledge varies is usually as necessary. In climate knowledge, for example, it exhibits you the way secure or risky the circumstances have been.
As a substitute of individually calling max() and min(), or manually subtracting. np.ptp() makes it concise, readable, and vectorised, particularly helpful once you’re computing ranges throughout a number of rows or columns.
Now, let’s apply this to our dataset.
Drawback: How a lot did the temperature fluctuate this week?
temps = np.array([30, 32, 29, 35, 36, 33, 31])
np.ptp(temps)Output: np.int64(7)
This tells us the temperature fluctuated by 7°C over the interval, from 29°C to 36°C.
4. np.diff() — Detect Each day Adjustments
np.diff() is the quickest solution to measure momentum, development, or decline throughout time. It mainly calculates variations between components in an array.
To color an image for you, in case your dataset have been a journey, np.ptp() tells you the way far you’ve travelled total, whereas np.diff() tells you the way far you moved between every cease.
Primarily:
np.diff([a1, a2, a3, …]) = [a2 — a1, a3 — a2, …]
Let’s apply this to our dataset.
Let’s have a look at our temperature knowledge once more:
temps = np.array([30, 32, 29, 35, 36, 33, 31])
daily_change = np.diff(temps)
print(daily_change)Output: [ 2 -3 6 1 -3 -2]
In the actual world, np.diff() is used for
- Time collection evaluation — Observe each day adjustments in temperature, gross sales, or inventory costs.
- Sign processing — Determine spikes or sudden drops in sensor knowledge.
- Information validation — Detect jumps or inconsistencies between consecutive measurements.
5. np.gradient() — Seize Clean Traits and Slopes
To be sincere, once I first got here throughout this, i discovered it arduous to understand. However primarily, np.gradient() computes the numerical gradient (a easy estimate of change or slope) throughout your knowledge. It’s much like np.diff(), nevertheless, np.gradient() works even when your x-values are erratically spaced (e.g., irregular timestamps). It supplies a smoother sign, making traits simpler to interpret visually.
For example:
time = np.array([0, 1, 2, 4, 7])
temp = np.array([30, 32, 34, 35, 36])
np.gradient(temp, time)Output: array([2. , 2. , 1.5 , 0.43333333, 0.33333333])
Let’s break this down a bit.
Usually, np.gradient() assumes the x-values (your index positions) are evenly spaced — like 0, 1, 2, 3, 4, and many others. However within the instance above, the time array isn’t evenly spaced: discover the jumps are 1, 1, 2, 3. Meaning temperature readings weren’t taken each hour.
By passing time because the second argument, we’re primarily telling NumPy to make use of the precise time gaps when calculating how briskly temperature adjustments.
To elucidate the output above. It’s saying between 0–2 hours, the temperature rose rapidly (about 2°C per hour), and between 2–7 hours, the rise slowed all the way down to round 0.3–1°C per hour.
Let’s apply this to our dataset.
Drawback: Estimate the speed of temperature change (like slope).
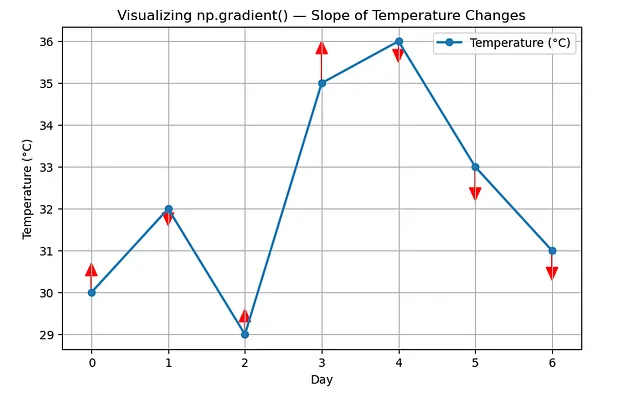
temps = np.array([30, 32, 29, 35, 36, 33, 31])
grad = np.gradient(temps)
np.spherical(grad, 2)Output: array([ 2. , -0.5, 1.5, 3.5, -1. , -2.5, -2. ])
You’ll be able to learn it like:
- +2 → temp rising quick (early warm-up)
- -0.5 → slight drop (minor cooling)
- +1.5, +3.5 → robust rise (large warmth bounce)
- -1, -2.5, -2 → regular cooling pattern
So this tells a narrative of the week’s temperature. Let’s visualise this actual fast with matplotlib.
Discover how straightforward it’s to interpret the visualisation. That’s what makes np.gradient() so helpful.
6. np.percentile() – Spot Outliers or Thresholds
That is one among my favorite features. np.percentile() helps you retrieve chunks or slices of your knowledge. Numpy defines it properly.
numpy.percentile computes the q-th percentile of knowledge alongside a specified axis, the place q is a proportion between 0 and 100.
In np.percentile(), often there’s a threshold to fulfill (which is 100%). You’ll be able to then stroll backwards and examine the proportion of information that fall under this threshold.
Let’s do this out with gross sales information
Let’s say your month-to-month gross sales goal is $60,000.
You should use np.percentile() to grasp how typically and the way strongly you’re hitting or lacking that focus on.
import numpy as np
gross sales = np.array([45, 50, 52, 48, 60, 62, 58, 70, 72, 66, 63, 80])
np.percentile(gross sales, [25, 50, 75, 90])Output: [51.0 61.0 67.5 73.0]
To interrupt this down:
- twenty fifth percentile = $51k → 25% of your months have been under ₦51k (low performers)
- fiftieth percentile = $61k → half of your months have been under ₦61k (round your goal)
- seventy fifth percentile = $67.5k → top-performing months are comfortably above goal
- ninetieth percentile = $73k → your finest months hit ₦73k or extra
So now you’ll be able to say:
“We hit or exceeded our $60k goal in roughly half of all months.”
This can be visualised utilizing a KPI card. That’s fairly highly effective.
That’s KPI storytelling with knowledge.
Let’s apply that to our temperature dataset.
import numpy as np
temps = np.array([30, 32, 29, 35, 36, 33, 31])
np.percentile(temps, [25, 50, 75])Output: [30.5 32. 34.5]
Right here’s what it means:
- 25% of the readings are under 30.5°C
- 50% (the median) are under 32°C
- 75% are under 34.5°C
7. np.distinctive() — Shortly Discover Distinctive Values and Their Counts
This operate is ideal for cleansing, summarising, or categorising knowledge. np.distinctive() finds all of the distinctive components in your array. It will probably additionally examine how typically these components seem in your array.
For example, let’s say you could have a listing of product classes out of your retailer:
import numpy as np
merchandise = np.array([
‘Shoes’, ‘Bags’, ‘Bags’, ‘Hats’,
‘Shoes’, ‘Shoes’, ‘Belts’, ‘Hats’
])
np.distinctive(merchandise)Output: array([‘Bags’, ‘Belts’, ‘Hats’, ‘Shoes’], dtype=’<U5′)
You’ll be able to take issues additional by counting the variety of occasions they seem utilizing the return_counts property:
np.distinctive(merchandise, return_counts=True)Output: (array([‘Bags’, ‘Belts’, ‘Hats’, ‘Shoes’], dtype=’<U5′), array([2, 1, 2, 3])).
Let’s apply that to my temperature dataset. Presently, there aren’t any duplicates, so we’re simply gonna get our similar enter again.
import numpy as np
temps = np.array([30, 32, 29, 35, 36, 33, 31])
np.distinctive(temps)Output: array([29, 30, 31, 32, 33, 35, 36])
Discover how the figures are organised accordingly, too — in ascending order.
It’s also possible to ask NumPy to depend what number of occasions every worth seems:
np.distinctive(temps, return_counts=True)Output: (array([29, 30, 31, 32, 33, 35, 36]), array([1, 1, 1, 1, 1, 1, 1]))
Wrapping up
Thus far, these are the features I stumbled upon. And I discover them to be fairly useful in knowledge evaluation. The fantastic thing about NumPy is that the extra you play with it, the extra you uncover these tiny one-liners that substitute pages of code. So subsequent time you’re wrangling knowledge or debugging a messy dataset, steer clear of Pandas for a bit, and take a look at dropping in one among these features. Thanks for studying!