scientist inevitably means engaged on a number of layers of abstraction, foremost abstractions of code and math. That is nice, as a result of this lets you get astonishing outcomes rapidly. However typically it’s well-advised to pause for a second and ponder what truly occurs behind a neat interface. This technique of pondering is commonly assisted by visualizations. On this article, I need to current how animated quiver plots may also help to ponder about linear transformations, which frequently toil away reliably within the obscurity of machine studying algorithms and related interfaces. In the long run, we will visualize ideas like Singular Worth Decomposition with our quiver plot.
Plotting Static Quiver Plots
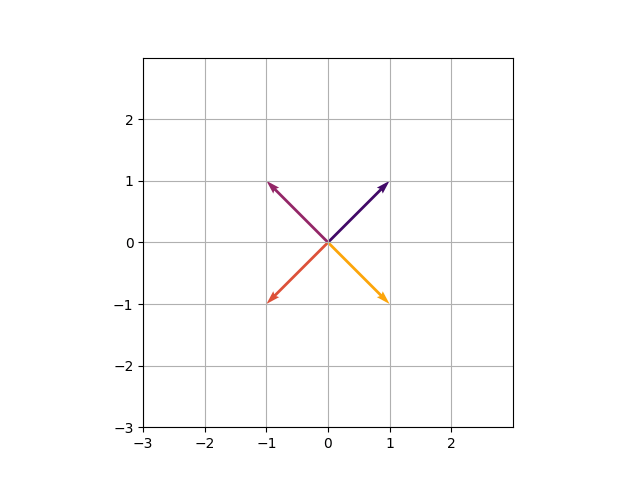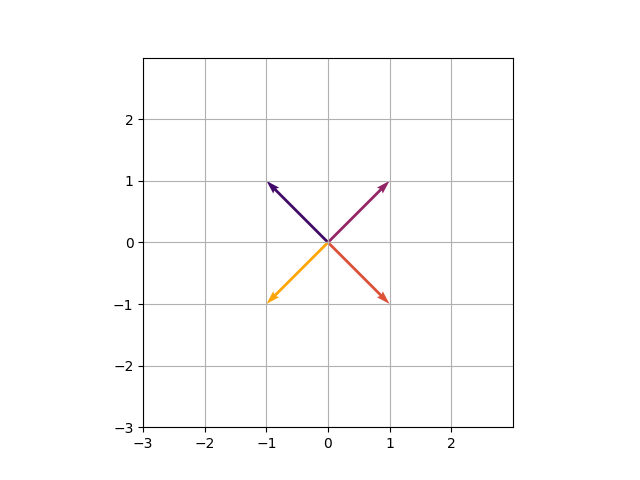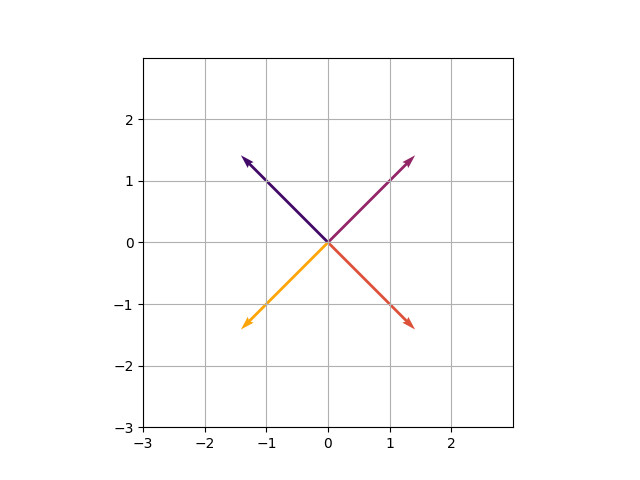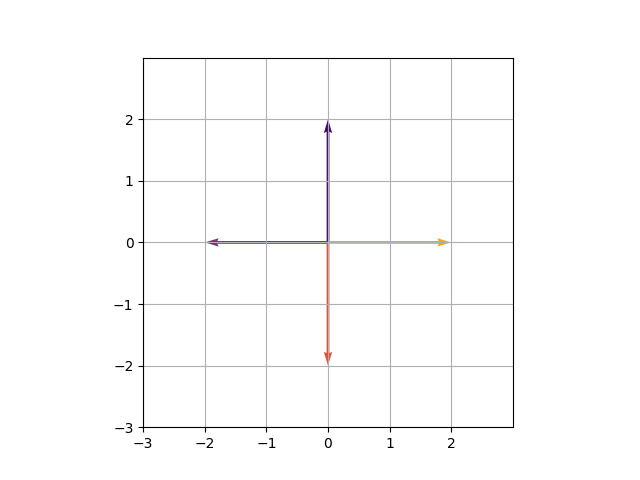
A quiver plot from the matplotlib python package deal permits us to plot arrows (which in our case signify vectors). Let’s first check out a static quiver plot:
We will instantly derive the transformation matrix from the picture by wanting on the goal positions of the 2 base vectors. The primary base vector is beginning at place (1, 0) and touchdown on (1, 1), whereas the second base vector travels from (0, 1) to (-1, 1). Due to this fact the matrix, that describes this transformation is:
[
begin{pmatrix}
1 & -1
1 & 1
end{pmatrix}
]
Visually this corresponds to an anti-clockwise rotation by 45 levels (or (pi/4) in radian) and a slight stretch (by the issue (sqrt{2})).
With this data, let’s have a look at how that is carried out with quiver (Be aware that I omit some boilerplate code like scaling of axis):
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
def quiver_plot_base_vectors(transformation_matrix: np.ndarray):
# Outline vectors
basis_i = np.array([1, 0])
basis_j = np.array([0, 1])
i_transformed = transformation_matrix[:, 0]
j_transformed = transformation_matrix[:, 1]
# plot vectors with quiver-function
cmap = cm.inferno
fig, ax = plt.subplots()
ax.quiver(0, 0, basis_i[0], basis_i[1],
colour=cmap(0.2),
scale=1,
angles="xy",
scale_units="xy",
label="i",
alpha=0.3)
ax.quiver(0, 0, i_transformed[0], i_transformed[1],
colour=cmap(0.2),
scale=1,
angles="xy",
scale_units="xy",
label="i_transformed")
ax.quiver(0, 0, basis_j[0], basis_j[1],
colour=cmap(0.5),
scale=1,
angles="xy",
scale_units="xy",
label="j",
alpha=0.3)
ax.quiver(0, 0, j_transformed[0], j_transformed[1],
colour=cmap(0.5),
scale=1,
angles="xy",
scale_units="xy",
label="j_transformed")
if __name__ == "__main__":
matrix = np.array([
[1, -1],
[1, 1]
])
quiver_plot_base_vectors(matrix)As you’ll be able to see we outlined one quiver plot per vector. That is only for illustrative functions. If we have a look at the signature of the quiver perform – quiver([X, Y], U, V, [C], /, **kwargs) – we will observe that U and V take numpy arrays as enter, which is healthier than offering scalar values. Let’s refactor this perform to utilizing just one quiver invocation. Moreover, let’s add a vector v = (1.5, -0.5) to see the transformation utilized on it.
def quiver_plot(transformation_matrix: np.ndarray, vector: np.ndarray):
# Outline vectors
basis_i = np.array([1, 0])
basis_j = np.array([0, 1])
i_transformed = transformation_matrix[:, 0]
j_transformed = transformation_matrix[:, 1]
vector_transformed = transformation_matrix @ vector
U, V = np.stack(
[
basis_i, i_transformed,
basis_j, j_transformed,
vector, vector_transformed,
],
axis=1)
# Draw vectors
colour = np.array([.2, .2, .5, .5, .8, .8])
alpha = np.array([.3, 1.0, .3, 1.0, .3, 1.0])
cmap = cm.inferno
fig, ax = plt.subplots()
ax.quiver(np.zeros(6), np.zeros(6), U, V,
colour=cmap(colour),
alpha=alpha,
scale=1,
angles="xy",
scale_units="xy",
)
if __name__ == "__main__":
matrix = np.sqrt(2) * np.array([
[np.cos(np.pi / 4), np.cos(3 * np.pi / 4)],
[np.sin(np.pi / 4), np.sin(3 * np.pi / 4)]
])
vector = np.array([1.5, -0.5])
quiver_plot(matrix, vector)That is a lot shorter and handy than the primary instance. What we did right here was to stack every vector horizontally producing the next array:

The primary row corresponds to the U-parameter of quiver and the second to V. Whereas the columns maintain our vectors, the place (vec{i}) is the primary base vector, (vec{j}) is the second and (vec{v}) is our customized vector. The indices, b and a, stand for earlier than and after (i.e. whether or not the linear transformation is utilized or not). Let’s have a look at the output:

Picture by Writer
Taking a second have a look at the code it may be complicated what occurred to our neat and easy transformation matrix, which was restated to:
[
{scriptsize
M=begin{pmatrix}
{1}&{-1}
{1}&{1}
end{pmatrix}={sqrt{2}}
begin{pmatrix}
{cosleft(frac{1}{4}piright)}&{cosleft(frac{3}{4}piright)}
{sinleft(frac{1}{4}piright)}&{sinleft(frac{3}{4}piright)}
end{pmatrix}
}
]
The reason being, as we transfer on by including animations, this illustration will come in useful. The scalar multiplication by the sq. root of two represents how a lot our vectors get stretched, whereas the weather of the matrix are rewritten in trigonometric notation to depict the rotation within the unit circle.
Let’s animate
Causes so as to add animations might embrace cleaner plots as we will do away with the ghost vectors and create a extra partaking expertise for shows. With a purpose to improve our plot with animations we will keep within the matplotlib ecosystem by using the FuncAnimation() perform from matplotlib.animation. The perform takes the next arguments:
- a
matplotlib.determine.Determineobject - an replace perform
- the variety of frames
For every body the replace perform will get invoked producing an up to date model of the preliminary quiver plot. For extra particulars verify the official documentation from matplotlib.
With this data in thoughts our activity is to outline the logic to implement within the replace perform. Let’s begin easy with solely three frames and our base vectors. On body 0 we’re within the preliminary state. Whereas on the final body (body 2) we have to arrive on the restated matrix M. Due to this fact we’d anticipate to be half method there on body 1. As a result of the arguments of (cos) and (sin) in M present the radians (i.e. how far we’ve traveled on the unit circle), we will divide them by two to be able to get our desired rotation. (The second vector will get a damaging (cos) , as a result of we are actually within the second quadrant). Equally we have to account for the stretch, represented by the scalar issue. We do that by computing the change in magnitude, which is (sqrt{2}-1), and including half of that change to the preliminary scaling.
[
{scriptsize
begin{aligned}
text{Frame 0:} quad &
begin{pmatrix}
cos(0) & cosleft(frac{pi}{2}right)
sin(0) & sinleft(frac{pi}{2}right)
end{pmatrix}
[1em]
textual content{Body 1:} quad &
s cdot start{pmatrix}
cosleft(frac{1}{2} cdot frac{pi}{4}proper) & -cosleft(frac{1}{2} cdot frac{3pi}{4}proper)
sinleft(frac{1}{2} cdot frac{pi}{4}proper) & sinleft(frac{1}{2} cdot frac{3pi}{4}proper)
finish{pmatrix}, quad textual content{with } s = 1 + frac{sqrt{2} – 1}{2}
[1em]
textual content{Body 2:} quad &
sqrt{2} cdot start{pmatrix}
cosleft(frac{pi}{4}proper) & cosleft(frac{3pi}{4}proper)
sinleft(frac{pi}{4}proper) & sinleft(frac{3pi}{4}proper)
finish{pmatrix}
finish{aligned}
}
]

GIF by Writer
One Caveat to the reason above: It serves the aim to offer instinct to the implementation concept and holds true for the bottom vectors. Nevertheless the precise implementation comprises some extra steps, e.g. some transformations with (arctan) to get the specified habits for all vectors within the two-dimensional area.
So let’s examine the principle elements of the implementation. The complete code could be discovered on my github.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
from matplotlib import cm
class AnimationPlotter:
[...]
def animate(self, filename='output/mat_transform.gif'):
self.initialize_plot()
anim = animation.FuncAnimation(
self.fig,
self.update_quiver,
frames=self.frames + 1,
init_func=self.init_quiver,
blit=True,
)
anim.save(filename, author='ffmpeg', fps=self.frames/2)
plt.shut()
if __name__ == "__main__":
matrix = np.sqrt(2) * np.array([
[np.cos(np.pi / 4), np.cos(3 * np.pi / 4)],
[np.sin(np.pi / 4), np.sin(3 * np.pi / 4)]
])
vector = np.array([1.5, -0.5]).reshape(2, 1)
transformer = Transformer(matrix)
animation_plotter = AnimationPlotter(transformer, vector)
animation_plotter.animate()The animate() technique belongs to a customized class, which is known as AnimationPlotter. It does what we already discovered with the inputs as offered above. The second class on the scene is a customized class Transformer, which takes care of computing the linear transformations and intermediate vectors for every body. The principle logic lies throughout the AnimationPlotter.update_quiver() and Transformer.get_intermediate_vectors() strategies, and appears as follows.
class AnimationPlotter:
[...]
def update_quiver(self, body: int):
incremented_vectors = self.transformer.get_intermediate_vectors(
body, self.frames
)
u = incremented_vectors[0]
v = incremented_vectors[1]
self.quiver_base.set_UVC(u, v)
return self.quiver_base,
class Transformer:
[...]
def get_intermediate_vectors(self, body: int, total_frames: int) -> np.ndarray:
change_in_direction = self.transformed_directions - self.start_directions
change_in_direction = np.arctan2(np.sin(change_in_direction), np.cos(change_in_direction))
increment_direction = self.start_directions + change_in_direction * body / total_frames
increment_magnitude = self.start_magnitudes + (self.transformed_magnitudes - self.start_magnitudes) * body / total_frames
incremented_vectors = np.vstack([np.cos(increment_direction), np.sin(increment_direction)]) @ np.diag(increment_magnitude)
return incremented_vectorsWhat occurs right here is that for every body the intermediate vectors get computed. That is accomplished by taking the distinction between the tip and begin instructions (which signify vector angles). The change in course/angle is then normalized to the vary ([-pi, pi]) and added to the preliminary course by a ratio. The ratio is decided by the present and whole frames. The magnitude is decided as already described. Lastly, the incremented vector will get computed primarily based on the course and magnitude and that is what we see at every body within the animation. Growing the frames to say 30 or 60 makes the animation easy.
Animating Singular Worth Decomposition (SVD)
Lastly I need to showcase how the introductory animation was created. It exhibits how 4 vectors (every for each quadrant) get remodeled consecutively thrice. Certainly, the three transformations utilized correspond to our in the meantime well-known transformation matrix M from above, however decomposed through Singular Worth Decomposition (SVD). You possibly can achieve or refresh your information about SVD in this nice and intuitive tds article. Or have a look here for those who want a extra math-focused learn. Nevertheless, with numpy.linalg.svd() it’s simple to compute the SVD of our matrix M. Doing so ends in the next decomposition:
[
{scriptsize
begin{align}
A vec{v} &= USigma V^Tvec{v} [1em]
sqrt{2} cdot start{pmatrix}
cosleft(frac{pi}{4}proper) & cosleft(frac{3pi}{4}proper)
sinleft(frac{pi}{4}proper) & sinleft(frac{3pi}{4}proper)
finish{pmatrix} vec{v} &=
start{pmatrix}
cosleft(frac{3pi}{4}proper) & cosleft(frac{3pi}{4}proper)
sinleft(frac{-pi}{4}proper) & sinleft(frac{pi}{4}proper)
finish{pmatrix}
start{pmatrix}
sqrt{2} & 0
0 & sqrt{2}
finish{pmatrix}
start{pmatrix}
-1 & 0
0 & 1
finish{pmatrix} vec{v}
finish{align}
}
]
Be aware how the stretching by the sq. root will get distilled by the center matrix. The next animation exhibits how this appears in motion (or movement) for v = (1.5, -0.5).

In the long run the purple vector (vec{v}) arrives at its decided place in each circumstances.
Conclusion
To wrap it up, we will use quiver() to show vectors in 2D area and, with the assistance of matplotlib.animation.FuncAnimation(), add interesting animations on prime. This ends in clear visualizations of linear transformations that you should use, as an example, to show the underlying mechanics of your machine studying algorithms. Be at liberty to fork my repository and implement your individual visualizations. I hope you loved the learn!