In my previous post I seemed on the influence of various hyperparameters on determination timber, each their efficiency and the way they seem visually.
The pure subsequent step, then, is random forests, utilizing sklearn.ensemble.RandomForestRegressor.
Once more, I gained’t go into how the random forests work, areas reminiscent of bootstrapping and have choice and majority voting. Basically, a random forest is a large variety of timber working collectively (therefore a forest), and that’s all we care about.
I’ll use the identical information (California housing dataset by way of scikit-learn, CC-BY) and the identical common course of, so when you haven’t seen my earlier put up, I’d recommend studying that first, because it goes over a number of the features and metrics I’m utilizing right here.
Code for that is in the identical repo as earlier than: https://github.com/jamesdeluk/data-projects/tree/main/visualising-trees
As earlier than, all pictures under are created by me.
A primary forest
First, let’s see how a primary random forest performs, i.e. rf = RandomForestRegressor(random_state=42). The default mannequin has an infinite max depth, and 100 timber. Utilizing the average-of-ten technique, it took ~6 seconds to suit and ~0.1 seconds to foretell – given it’s a forest and never a single tree, it’s not shocking it took 50 to 150 instances longer than the deep determination tree. And the scores?
| Metric | max_depth=None |
|---|---|
| MAE | 0.33 |
| MAPE | 0.19 |
| MSE | 0.26 |
| RMSE | 0.51 |
| R² | 0.80 |
It predicted 0.954 for my chosen row, in contrast with the precise worth of 0.894.
Sure, the out-of-the-box random forest carried out higher than the Bayes-search-tuned determination tree from my earlier put up!
Visualising
There are just a few methods to visualise a random forest, such because the timber, the predictions, and the errors. Characteristic importances can be used to match the person timber in a forest.
Particular person tree plots
Pretty clearly, you may plot a person determination tree. They are often accessed utilizing rf.estimators_. For instance, that is the primary one:
This one has a depth of 34, 9,432 leaves, and 18,863 nodes. And this random forest has 100 comparable timber!
Particular person predictions
A technique I wish to visualise random forests is plotting the person predictions for every tree. For instance, I can achieve this for my chosen row with [tree.predict(chosen[features].values) for tree in rf.estimators_], and plot the outcomes on a scatter:

As a reminder, the true worth is 0.894. You’ll be able to simply see how, whereas some timber have been method off, the imply of all of the predictions is fairly shut — just like the central restrict theorem (CLT). That is my favorite method of seeing the magic of random forests.
Particular person errors
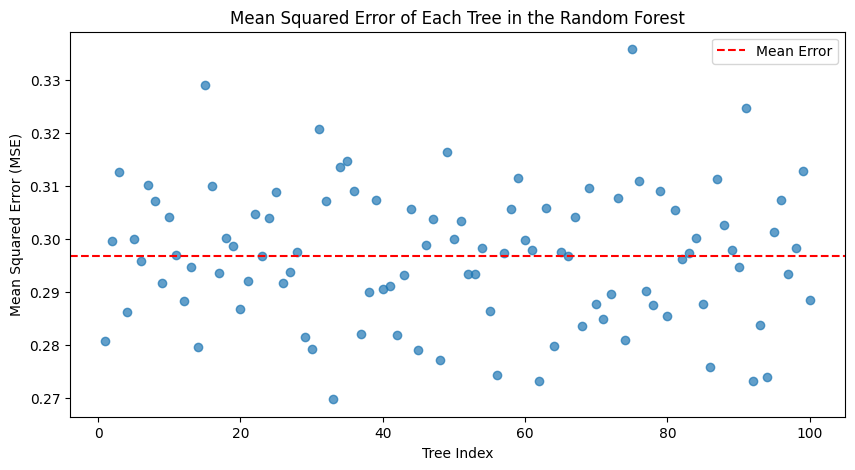
Taking this one step additional, you may iterate by means of all of the timber, have them make predictions for the whole dataset, then calculate an error statistic. On this case, for MSE:

The imply MSE was ~0.30, so barely larger than the general random forest — once more exhibiting the benefit of a forest over a single tree. The most effective tree was quantity 32, with an MSE of 0.27; the worst, 74, was 0.34 — though nonetheless fairly respectable. They each have depths of 34±1, with ~9400 leaves and ~18000 nodes — so, structurally, very comparable.
Characteristic importances
Clearly a plot with all of the timber can be troublesome to see, so that is the importances for the general forest, with the very best and worst tree:

The most effective and worst timber nonetheless have comparable importances for the totally different options — though the order just isn’t essentially the identical. Median earnings is by far a very powerful issue based mostly on this evaluation.
Hyperparameter tuning
The identical hyperparameters that apply to particular person determination timber do, after all, apply to random forests made up of determination timber. For comparability’s sake, I created some RFs with the values I’d used within the earlier put up:
| Metric | max_depth=3 | ccp_alpha=0.005 | min_samples_split=10 | min_samples_leaf=10 | max_leaf_nodes=100 |
|---|---|---|---|---|---|
| Time to suit (s) | 1.43 | 25.04 | 3.84 | 3.77 | 3.32 |
| Time to foretell (s) | 0.006 | 0.013 | 0.028 | 0.029 | 0.020 |
| MAE | 0.58 | 0.49 | 0.37 | 0.37 | 0.41 |
| MAPE | 0.37 | 0.30 | 0.22 | 0.22 | 0.25 |
| MSE | 0.60 | 0.45 | 0.29 | 0.30 | 0.34 |
| RMSE | 0.78 | 0.67 | 0.54 | 0.55 | 0.58 |
| R² | 0.54 | 0.66 | 0.78 | 0.77 | 0.74 |
| Chosen prediction | 1.208 | 1.024 | 0.935 | 0.920 | 0.969 |
The very first thing we see — none carried out higher than the default tree (max_depth=None) above. That is totally different from the person determination timber, the place those with constraints carried out higher — once more demonstrating that the ability of a CLT-powered imperfect forest over one “excellent” tree. Nonetheless, just like earlier than, ccp_alpha takes a very long time, and shallow timber are fairly garbage.
Past these, there are some hyperparameters that RFs have that DTs don’t. An important one is n_estimators — in different phrases, the variety of timber!
n_jobs
However first, n_jobs. That is what number of jobs to run in parallel. Doing issues in parallel is usually sooner than in serial/sequentially. The ensuing RF would be the similar, with the identical error and many others scores (assuming random_state is about), but it surely must be finished faster! To check this, I added n_jobs=-1 to the default RF — on this context, -1 means “all”.
Keep in mind how the default one took virtually 6 seconds to suit and 0.1 to foretell? Parallelised, it took only one.1 seconds, and 0.03 to foretell — a 3~6x enchancment. I’ll undoubtedly be doing this any further!
n_estimators
OK, again to the variety of timber. The default RF has 100 estimators; let’s attempt 1000. It took ~10 instances as lengthy (9.7 seconds to suit, 0.3 to foretell, when parallelised), as one might need predicted. The scores?
| Metric | n_estimators=1000 |
|---|---|
| MAE | 0.328 |
| MAPE | 0.191 |
| MSE | 0.252 |
| RMSE | 0.502 |
| R² | 0.807 |
Little or no distinction; MSE and RMSE are 0.01 decrease, and R² is 0.01 larger. So higher, however well worth the 10x time funding?
Let’s cross-validate, simply to test.
Moderately than use my customized loop, I’ll use sklearn.model_selection.cross_validate, as touched on within the earlier put up:
cross_validate(
rf, X, y,
cv=RepeatedKFold(n_splits=5, n_repeats=20, random_state=42),
n_jobs=-1,
scoring={
"neg_mean_absolute_error": "neg_mean_absolute_error",
"neg_mean_absolute_percentage_error": "neg_mean_absolute_percentage_error",
"neg_mean_squared_error": "neg_mean_squared_error",
"root_mean_squared_error": make_scorer(
lambda y_true, y_pred: np.sqrt(mean_squared_error(y_true, y_pred)),
greater_is_better=False,
),
"r2": "r2",
},
)
I’m utilizing RepeatedKFold because the splitting technique, which is extra secure however slower than KFold; because the dataset isn’t that large, I’m not too involved concerning the further time it should take.
As there isn’t a normal RMSE scorer, so I needed to create one with sklearn.metrics.make_scorer and a lambda perform.
For the choice timber, I did 1000 loops. Nonetheless, given the default random forest incorporates 100 timber, 1000 loops can be a lot of timber, and subsequently take a lot of time. I’ll attempt 100 (20 repeats of 5 splits) — nonetheless so much, however due to parallelisation it wasn’t too dangerous — the 100 timber model took 2mins (1304 seconds of unparallelised time), and the 1000 one took 18mins (10254s!) Virtually 100% CPU throughout all cores, and it received fairly toasty — it’s not typically my MacBook followers activate, however this maxed them out!
How do they examine? The 100-tree one:
| Metric | Imply | Std |
|---|---|---|
| MAE | -0.328 | 0.006 |
| MAPE | -0.184 | 0.005 |
| MSE | -0.253 | 0.010 |
| RMSE | -0.503 | 0.009 |
| R² | 0.810 | 0.007 |
and the 1000-tree one:
| Metric | Imply | Std |
|---|---|---|
| MAE | -0.325 | 0.006 |
| MAPE | -0.183 | 0.005 |
| MSE | -0.250 | 0.010 |
| RMSE | -0.500 | 0.010 |
| R² | 0.812 | 0.006 |
Little or no distinction — most likely not value the additional time/energy.
Bayes looking out
Lastly, let’s do a Bayes search. I used a large hyperparameter vary.
search_spaces = {
'n_estimators': (50, 500),
'max_depth': (1, 100),
'min_samples_split': (2, 100),
'min_samples_leaf': (1, 100),
'max_leaf_nodes': (2, 20000),
'max_features': (0.1, 1.0, 'uniform'),
'bootstrap': [True, False],
'ccp_alpha': (0.0, 1.0, 'uniform'),
}The one hyperparameter we haven’t seen to this point is bootstrap; this determines whether or not to make use of the entire dataset when constructing a tree, or utilizing a bootstrap-based (pattern with alternative) strategy. Mostly that is set to True, however let’s attempt False anyway.
I did 200 iterations, which took 66 (!!) minutes. It gave:
Greatest Parameters: OrderedDict({
'bootstrap': False,
'ccp_alpha': 0.0,
'criterion': 'squared_error',
'max_depth': 39,
'max_features': 0.4863711682589259,
'max_leaf_nodes': 20000,
'min_samples_leaf': 1,
'min_samples_split': 2,
'n_estimators': 380
})See how max_depth was just like the straightforward ones above, however n_estimators and max_leaf_nodes have been very excessive (be aware max_leaf_nodes just isn’t the precise variety of leaf nodes, simply the utmost allowed worth; the imply variety of leaves was 14,954). min_samples_ have been each the minimal — just like earlier than after we in contrast the constrained forests to the unconstrained one. Additionally fascinating the way it didn’t bootstrap.
What does that give us (the short take a look at, not the cross validated one)?
| Metric | Worth |
|---|---|
| MAE | 0.313 |
| MAPE | 0.181 |
| MSE | 0.229 |
| RMSE | 0.478 |
| R² | 0.825 |
The most effective to this point, though solely simply. For consistency, I additionally cross validated:
| Metric | Imply | Std |
|---|---|---|
| MAE | -0.309 | 0.005 |
| MAPE | -0.174 | 0.005 |
| MSE | -0.227 | 0.009 |
| RMSE | -0.476 | 0.010 |
| R² | 0.830 | 0.006 |
It’s performing very properly. Evaluating absolutely the errors for the very best determination tree (the Bayes search one), the default RF, and the Bayes searched RF, offers us:

Conclusion
Within the final put up, the Bayes determination tree appeared good, particularly in contrast with the fundamental determination tree; now it appears horrible, with larger errors, decrease R², and wider variances! So why not all the time use a random forest?
Nicely, random forests do take so much longer to suit (and predict), and this turns into much more excessive with bigger datasets. Doing hundreds of tuning iterations on a forest with tons of of timber and a dataset of hundreds of thousands of rows and tons of of options… Even with parallelisation, it could actually take a very long time. It makes it fairly clear why GPUs, which concentrate on parallel processing, have turn out to be important for machine studying. Even so, it’s a must to ask your self — what is nice sufficient? Does the ~0.05 enchancment in MAE really matter in your use case?
Relating to visualisation, as with determination timber, plotting particular person timber could be a good option to get an thought of the general construction. Moreover, plotting the person predictions and errors is an effective way to see the variance of a random forest, and get a greater understanding of how they work.
However there are extra tree variants! Subsequent, gradient boosted ones.