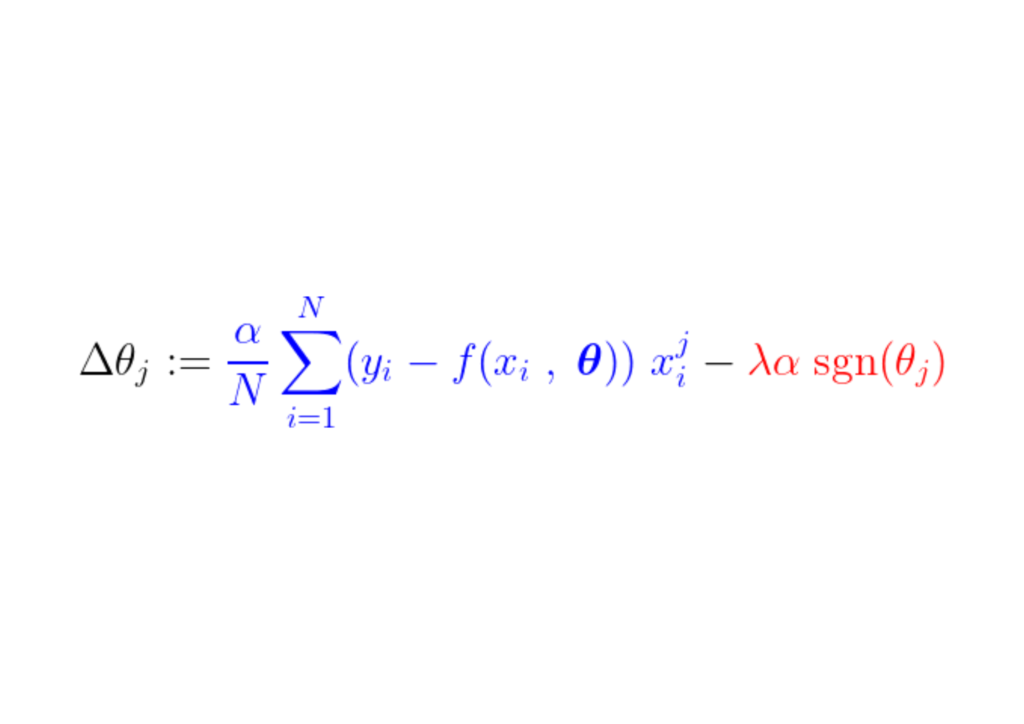is the method of choosing an optimum subset of options from a given set of options; an optimum function subset is the one which maximizes the efficiency of the mannequin on the given activity.
Function choice could be a guide or moderately express course of when carried out with filter or wrapper strategies. In these strategies, options are added or eliminated iteratively primarily based on the worth of a set measure, which quantifies the relevance of the function within the making the prediction. The measures may very well be data achieve, variance or the chi-squared statistic, and the algorithm would decide to just accept/reject the function contemplating a set threshold on the measure. Observe, these strategies should not part of the mannequin coaching stage and are carried out previous to it.
Embedded strategies carry out function choice implicitly, with out utilizing any pre-defined choice standards and deriving it from the coaching information itself. This intrinsic function choice course of is part of the mannequin coaching stage. The mannequin learns to pick options and make related predictions on the similar time. In later sections, we’ll describe the function of regularization in performing this intrinsic function choice.
Regularization and Mannequin Complexity
Regularization is the method of penalizing the complexity of the mannequin to keep away from overfitting and obtain generalization over the activity.
Right here, the complexity of the mannequin is analogous to its energy to adapt to the patterns within the coaching information. Assuming a easy polynomial mannequin in ‘x’ with diploma ‘d’, as we improve the diploma ‘d’ of the polynomial, the mannequin achieves higher flexibility to seize patterns within the noticed information.
Overfitting and Underfitting
If we try to suit a polynomial mannequin with d = 2 on a set of coaching samples which had been derived from a cubic polynomial with some noise, the mannequin won’t be able to seize the distribution of the samples to a adequate extent. The mannequin merely lacks the flexibility or complexity to mannequin the information generated from a level 3 (or greater order) polynomials. Such a mannequin is alleged to under-fit on the coaching information.
Engaged on the identical instance, assume we now have a mannequin with d = 6. Now with elevated complexity, it ought to be simple for the mannequin to estimate the unique cubic polynomial that was used to generate the information (like setting the coefficients of all phrases with exponent > 3 to 0). If the coaching course of isn’t terminated on the proper time, the mannequin will proceed to make the most of its further flexibility to cut back the error inside additional and begin capturing within the noisy samples too. It will scale back the coaching error considerably, however the mannequin now overfits the coaching information. The noise will change in real-world settings (or within the take a look at part) and any information primarily based on predicting them will disrupt, resulting in excessive take a look at error.
How you can decide the optimum mannequin complexity?
In sensible settings, now we have little-to-no understanding of the data-generation course of or the true distribution of the information. Discovering the optimum mannequin with the appropriate complexity, such that no under-fitting or overfitting happens is a problem.
One method may very well be to start out with a sufficiently highly effective mannequin after which scale back its complexity by way of function choice. Lesser the options, lesser is the complexity of the mannequin.
As mentioned within the earlier part, function choice may be express (filter, wrapper strategies) or implicit. Redundant options which have insignificant relevance within the figuring out the worth of the response variable ought to be eradicated to keep away from the mannequin studying uncorrelated patterns in them. Regularization, additionally performs the same activity. So, how are regularization and have choice linked to achieve a standard purpose of optimum mannequin complexity?
L1 Regularization As A Function Selector
Persevering with with our polynomial mannequin, we symbolize it as a operate f, with inputs x, parameters θ and diploma d,
For a polynomial mannequin, every energy of the enter x_i may be thought of as a function, forming a vector of the shape,

We additionally outline an goal operate, which on minimizing leads us to the optimum parameters θ* and features a regularization time period penalizing the complexity of the mannequin.

To find out the minima of this operate, we have to analyze all of its crucial factors i.e. factors the place the derivation is zero or undefined.
The partial spinoff w.r.t. one the parameters, θj, may be written as,

the place the operate sgn is outlined as,

Observe: The spinoff of absolutely the operate is totally different from the sgn operate outlined above. The unique spinoff is undefined at x = 0. We increase the definition to take away the inflection level at x = 0 and to make the operate differentiable throughout its whole area. Furthermore, such augmented features are additionally utilized by ML frameworks when the underlying computation entails absolutely the operate. Examine this thread on the PyTorch discussion board.
By computing the partial spinoff of the target operate w.r.t. a single parameter θj, and setting it to zero, we are able to construct an equation that relates the optimum worth of θj with the predictions, targets, and options.


Allow us to study the equation above. If we assume that the inputs and targets had been centered concerning the imply (i.e. the information had been standardized within the preprocessing step), the time period on the LHS successfully represents the covariance between the jth function and the distinction between the anticipated and goal values.
Statistical covariance between two variables quantifies how a lot one variable influences the worth of the second variable (and vice-versa)
The signal operate on the RHS forces the covariance on the LHS to imagine solely three values (because the signal operate solely returns -1, 0 and 1). If the jth function is redundant and doesn’t affect the predictions, the covariance will probably be almost zero, bringing the corresponding parameter θj* to zero. This ends in the function being eradicated from the mannequin.
Think about the signal operate as a canyon carved by a river. You possibly can stroll within the canyon (i.e. the river mattress) however to get out of it, you’ve got these large obstacles or steep slopes. L1 regularization induces the same ‘thresholding’ impact for the gradient of the loss operate. The gradient have to be highly effective sufficient to interrupt the obstacles or grow to be zero, which ultimately brings the parameter to zero.
For a extra grounded instance, contemplate a dataset that comprises samples derived from a straight line (parameterized by two coefficients) with some added noise. The optimum mannequin should not have any greater than two parameters, else it can adapt to the noise current within the information (with the added freedom/energy to the polynomial). Altering the parameters of the upper powers within the polynomial mannequin doesn’t have an effect on the distinction between the targets and the mannequin’s predictions, thus decreasing their covariance with the function.
Through the coaching course of, a relentless step will get added/subtracted from the gradient of the loss operate. If the gradient of the loss operate (MSE) is smaller than the fixed step, the parameter will ultimately attain to a worth of 0. Observe the equation under, depicting how parameters are up to date with gradient descent,


If the blue half above is smaller than λα, which itself is a really small quantity, Δθj is the almost a relentless step λα. The signal of this step (crimson half) is determined by sgn(θj), whose output is determined by θj. If θj is optimistic i.e. higher than ε, sgn(θj) equals 1, therefore making Δθj approx. equal to –λα pushing it in the direction of zero.
To suppress the fixed step (crimson half) that makes the parameter zero, the gradient of the loss operate (blue half) needs to be bigger than the step dimension. For a bigger loss operate gradient, the worth of the function should have an effect on the output of the mannequin considerably.
That is how a function is eradicated, or extra exactly, its corresponding parameter, whose worth doesn’t correlate with the output of the mannequin, is zero-ed by L1 regularization through the coaching.
Additional Studying And Conclusion
- To get extra insights on the subject, I’ve posted a query on r/MachineLearning subreddit and the ensuing thread comprises totally different explanations that you could be need to learn.
- Madiyar Aitbayev additionally has an interesting blog masking the identical query, however with a geometrical clarification.
- Brian Keng’s blog explains regularization from a probabilistic perspective.
- This thread on CrossValidated explains why L1 norm encourages sparse fashions. An in depth blog by Mukul Ranjan explains why L1 norm encourages the parameters to grow to be zero and never the L2 norm.
“L1 regularization performs function choice” is a straightforward assertion that almost all ML learners agree with, with out diving deep into the way it works internally. This weblog is an try to carry my understanding and mental-model to the readers in an effort to reply the query in an intuitive method. For ideas and doubts, yow will discover my e-mail at my website. Continue to learn and have a pleasant day forward!