Someday, an information scientist instructed that Ridge Regression was a sophisticated mannequin. As a result of he noticed that the coaching system is extra sophisticated.
Effectively, that is precisely the target of my Machine Learning “Advent Calendar”, to make clear this type of complexity.
So, ile, we are going to discuss penalized variations of linear regression.
- First, we are going to see why the regularization or penalization is important, and we are going to see how the mannequin is modified
- Then we are going to discover several types of regularization and their results.
- We will even practice the mannequin with regularization and check totally different hyperparameters.
- We will even ask an additional query about the way to weight the weights within the penalization time period. (confused ? You will notice)
Linear regression and its “circumstances”
Once we discuss linear regression, folks usually point out that some circumstances must be happy.
You could have heard statements like:
- the residuals must be Gaussian (it’s generally confused with the goal being Gaussian, which is fake)
- the explanatory variables shouldn’t be collinear
In classical statistics, these circumstances are required for inference. In machine studying, the main focus is on prediction, so these assumptions are much less central, however the underlying points nonetheless exist.
Right here, we are going to see an instance of two options being collinear, and let’s make them fully equal.
And we’ve the connection: y = x1 + x2, and x1 = x2
I do know that if they’re fully equal, we are able to simply do: y=2*x1. However the thought is to say they are often very comparable, and we are able to at all times construct a mannequin utilizing them, proper?
Then what’s the downside?
When options are completely collinear, the answer shouldn’t be distinctive. Right here is an instance within the screenshot beneath.
y = 10000*x1 – 9998*x2
And we are able to discover that the norm of the coefficients is large.
So, the concept is to restrict the norm of the coefficients.
And after making use of the regularization, the conceptual mannequin is identical!
That’s proper. The parameters of the linear regression are modified. However the mannequin is identical.
Completely different Variations of Regularization
So the concept is to mix the MSE and the norm of the coefficients.
As a substitute of simply minimizing the MSE, we attempt to decrease the sum of the 2 phrases.
Which norm? We will do with norm L1, L2, and even mix them.
There are three classical methods to do that, and the corresponding mannequin names.
Ridge regression (L2 penalty)
Ridge regression provides a penalty on the squared values of the coefficients.
Intuitively:
- massive coefficients are closely penalized (due to the sq.)
- coefficients are pushed towards zero
- however they by no means grow to be precisely zero
Impact:
- all options stay within the mannequin
- coefficients are smoother and extra steady
- very efficient in opposition to collinearity
Ridge shrinks, however doesn’t choose.

Lasso regression (L1 penalty)
Lasso makes use of a special penalty: the absolute worth of the coefficients.
This small change has a giant consequence.
With Lasso:
- some coefficients can grow to be precisely zero
- the mannequin routinely ignores some options
That is why LASSO known as so, as a result of it stands for Least Absolute Shrinkage and Choice Operator.
- Operator: it refers back to the regularization operator added to the loss perform
- Least: it’s derived from a least-squares regression framework
- Absolute: it makes use of absolutely the worth of the coefficients (L1 norm)
- Shrinkage: it shrinks coefficients towards zero
- Choice: it may set some coefficients precisely to zero, performing characteristic choice
Vital nuance:
- we are able to say that the mannequin nonetheless has the identical variety of coefficients
- however a few of them are pressured to zero throughout coaching
The mannequin type is unchanged, however Lasso successfully removes options by driving coefficients to zero.

3. Elastic Web (L1 + L2)
Elastic Web is a mixture of Ridge and Lasso.
It makes use of:
- an L1 penalty (like Lasso)
- and an L2 penalty (like Ridge)
Why mix them?
As a result of:
- Lasso will be unstable when options are extremely correlated
- Ridge handles collinearity effectively however doesn’t choose options
Elastic Web provides a steadiness between:
- stability
- shrinkage
- sparsity
It’s usually probably the most sensible selection in actual datasets.
What actually modifications: mannequin, coaching, tuning
Allow us to take a look at this from a Machine Studying viewpoint.
The mannequin does probably not change
For the mannequin, for all of the regularized variations, we nonetheless write:
y =a x + b.
- Identical variety of coefficients
- Identical prediction system
- However, the coefficients will probably be totally different.
From a sure perspective, Ridge, Lasso, and Elastic Web are not totally different fashions.
The coaching precept can be the identical
We nonetheless:
- outline a loss perform
- decrease it
- compute gradients
- replace coefficients
The one distinction is:
- the loss perform now features a penalty time period
That’s it.
The hyperparameters are added (that is the true distinction)
For Linear regression, we don’t have the management of the “complexity” of the mannequin.
- Normal linear regression: no hyperparameter
- Ridge: one hyperparameter (lambda)
- Lasso: one hyperparameter (lambda)
- Elastic Web: two hyperparameters
- one for general regularization energy
- one to steadiness L1 vs L2
So:
- normal linear regression doesn’t want tuning
- penalized regressions do
That is why normal linear regression is commonly seen as “probably not Machine Studying”, whereas regularized variations clearly are.
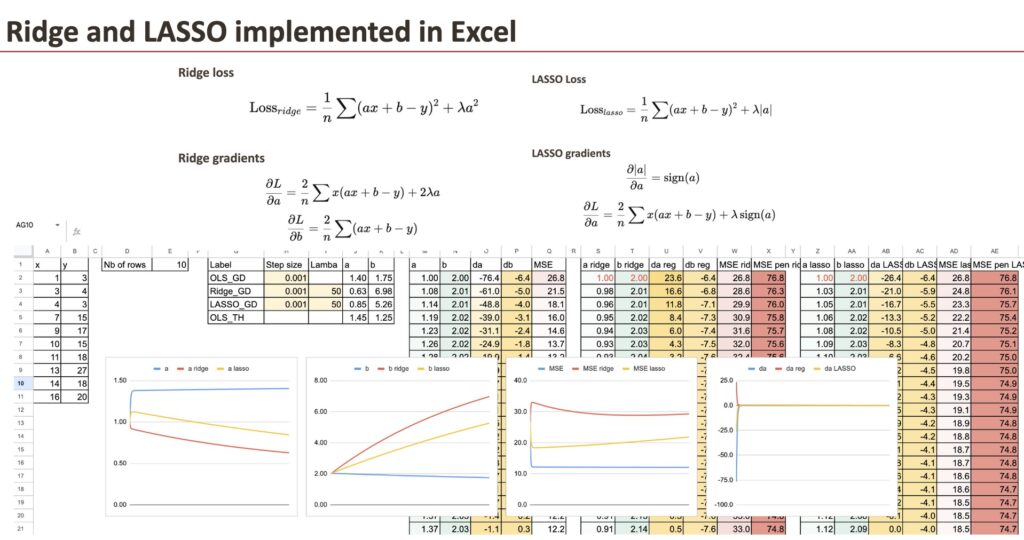
Implementation of Regularized gradients
We preserve the gradient descent of OLS regression as reference, and for Ridge regression, we solely have so as to add the regularization time period for the coefficient.
We’ll use a easy dataset that I generated (the identical one we already used for Linear Regression).
We will see the three “fashions” differ by way of coefficients. And the aim on this chapter is to implement the gradient for all of the fashions and examine them.

Ridge with penalized gradient
First, we are able to do for Ridge, and we solely have to vary the gradient of a.
Now, it doesn’t imply that the worth b shouldn’t be modified, for the reason that gradient of b is every step relies upon additionally on a.

LASSO with penalized gradient
Then we are able to do the identical for LASSO.
And the one distinction can be the gradient of a.
For every mannequin, we are able to additionally calculate the MSE and the regularized MSE. It’s fairly satisfying to see how they lower over the iterations.

Comparability of the coefficients
Now, we are able to visualize the coefficient a for all of the three fashions. As a way to see the variations, we enter very massive lambdas.

Affect of lambda
For giant worth of lambda, we are going to see that the coefficient a turns into small.
And if lambda LASSO turns into extraordinarily massive, then we theoretically get the worth of 0 for a. Numerically, we’ve to enhance the gradient descent.

Regularized Logistic Regression?
We noticed Logistic Regression yesterday, and one query we are able to ask is that if it can be regularized. If sure, how are they known as?
The reply is after all sure, Logistic Regression will be regularized
Precisely the identical thought applies.
Logistic regression can be:
- L1 penalized
- L2 penalized
- Elastic Web penalized
There are no particular names like “Ridge Logistic Regression” in widespread utilization.
Why?
As a result of the idea is not new.
In follow, libraries like scikit-learn merely allow you to specify:
- the loss perform
- the penalty sort
- the regularization energy
The naming mattered when the concept was new.
Now, regularization is simply an ordinary possibility.
Different questions we are able to ask:
- Is regularization at all times helpful?
- How does the scaling of options influence the efficiency of regularized linear regression?
Conclusion
Ridge and Lasso don’t change the linear mannequin itself, they alter how the coefficients are realized. By including a penalty, regularization favors steady and significant options, particularly when options are correlated. Seeing this course of step-by-step in Excel makes it clear that these strategies aren’t extra complicated, simply extra managed.