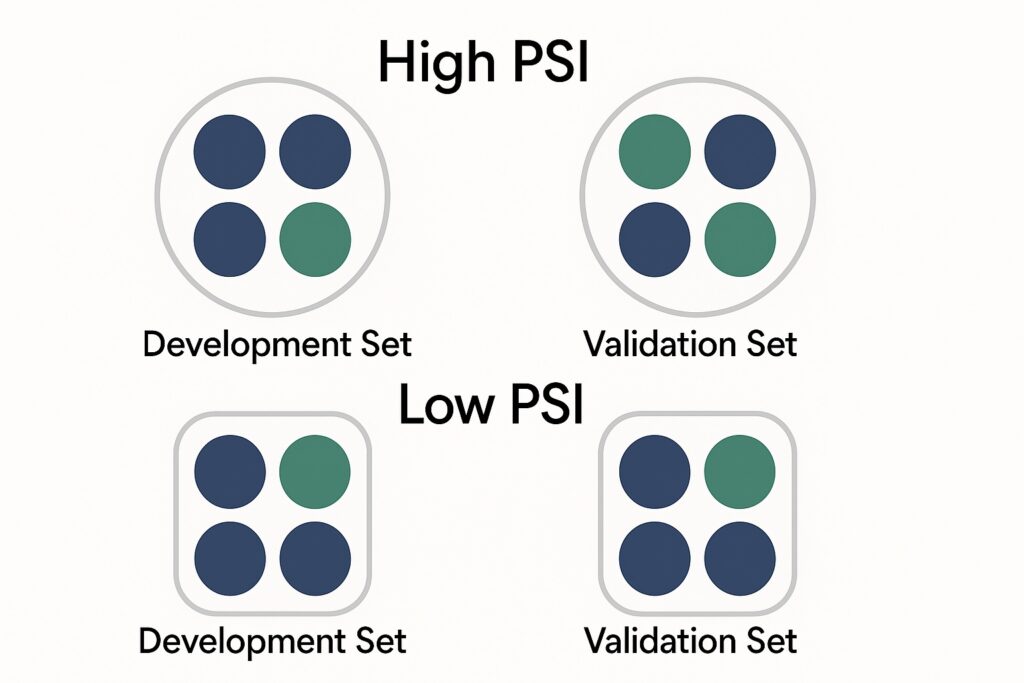
To get essentially the most out of this tutorial, it is best to have a strong understanding of methods to examine two distributions. When you don’t, I like to recommend trying out this glorious article by @matteo-courthoud.
We automated the evaluation and exported the outcomes to an Excel file utilizing Python. When you already know the fundamentals of Python and methods to write to Excel, that can make issues even simpler.
I want to thank everybody who took the time to learn and have interaction with my article. Your help and suggestions imply quite a bit.
, whether or not tutorial or skilled, the query of knowledge representativeness between two samples arises incessantly.
By representativeness, we imply the diploma to which two samples resemble one another or share the identical traits. This idea is important, because it immediately determines the accuracy of statistical conclusions or the efficiency of a predictive mannequin.
At every stage of a mannequin’s life cycle, the problem of knowledge representativeness takes particular varieties :
- Throughout the development part: that is the place all of it begins. You collect the information, clear it, break up it into coaching, check, and out-of-time samples, estimate the parameters, and punctiliously doc each determination. You make sure that the check and the out-of-time samples are consultant of the coaching information.
- In The appliance part: as soon as the mannequin is constructed, it have to be confronted with actuality. And right here a vital query arises: do the brand new datasets really resemble those used throughout development? If not, a lot of the earlier work could rapidly lose its worth.
- In the monitoring part, or backtesting: over time, populations evolve. The mannequin should due to this fact be repeatedly challenged. Do its predictions stay legitimate? Is the representativeness of the goal portfolio nonetheless ensured?
Representativeness is due to this fact not a one-off constraint, however a problem that accompanies the mannequin all through its improvement.
To reply the query of representativeness between two samples, the commonest method is to check their distributions, proportions, and constructions. This includes using visible instruments like density capabilities, histograms, boxplots, supplemented by statistical assessments such because the Scholar’s t-test, the Kruskal-Wallis check, the Wilcoxon check, or the Kolmogorov-Smirnov check. On this topic, @matteo-courthoud has printed an incredible article, full with sensible codes, to which we refer the reader for additional data.
On this article, we are going to deal with two sensible instruments typically utilized in credit score danger administration to test whether or not two datasets are comparable:
- The Inhabitants Stability Index (PSI) exhibits how a lot a distribution shifts, both over time or between two samples.
- Cramér’s V measures the power of affiliation between classes, serving to us see if two populations share an analogous construction.
We’ll then discover how these instruments might help engineers and decision-makers by remodeling statistical comparisons into clear information for quicker and extra dependable selections.
In Part 1 of this text, we current two concrete examples the place questions of representativeness between samples could come up. In Part 2, we consider representativeness between two datasets utilizing PSI and Cramér’s V. Lastly, in Part 3, we display methods to implement and automate these analyses in Python, exporting the outcomes into an Excel file.
1. Two real-world examples of the representativeness problem
The problem of representativeness turns into vital when a mannequin is utilized to a site aside from the one for which it was developed. Two typical conditions illustrate this problem:
1.1 When a mannequin is utilized to a new scope of shoppers
Think about a financial institution creating a scoring mannequin for small companies. The mannequin performs properly and is acknowledged internally. Inspired by this success, the management decides to increase its use to giant companies. Your supervisor asks on your opinion on the method. What steps do you’re taking earlier than responding?
Because the improvement and software populations differ, utilizing the mannequin on the brand new inhabitants extends its scope. It’s due to this fact essential to verify that this software is legitimate.
The statistician has a number of instruments to handle this query, specifically representativeness evaluation evaluating the event inhabitants with the appliance inhabitants. This may be completed by inspecting their traits variable by variable, for instance by means of assessments of imply equality, assessments of distribution equality, or by evaluating the distribution of categorical variables.
1.2 When two banks merge and have to align their danger fashions
Now contemplate Financial institution A, a big establishment with a considerable steadiness sheet and a confirmed mannequin to evaluate shopper default danger. Financial institution A is finding out the opportunity of merging with Financial institution B. Financial institution B, nevertheless, operates in a weaker financial setting and has not developed its personal inner mannequin.
Suppose Financial institution A’s administration approaches you, because the statistician chargeable for its inner fashions. The strategic query is: would it not be applicable to use Financial institution A’s inner fashions to Financial institution B’s portfolio within the occasion of a merger?
Earlier than making use of Financial institution A’s inner mannequin to Financial institution B’s portfolio, it’s essential to check the distributions of key variables throughout each portfolios. The mannequin can solely be transferred with confidence if the 2 populations are really consultant of one another.
Now we have simply offered two concrete instances the place verifying representativeness is important for sound decision-making. Within the subsequent part, we handle methods to analyze representativeness between two portfolios by introducing two statistical instruments: the Inhabitants Stability Index (PSI) and Cramér’s V.
2. Evaluating Distributions to Assess Representativeness Between Two Populations Utilizing the Inhabitants Stability Index (PSI) and V-Cramer.
In apply, the research of representativeness between two datasets consists of evaluating the traits of the noticed variables in each samples. This comparability depends on each statistical measures and visible instruments.
From a statistical perspective, analysts typically study measures of central tendency (imply, median) and dispersion (variance, commonplace deviation), in addition to extra granular indicators comparable to quantiles.
On the visible facet, widespread instruments embody histograms, boxplots, cumulative distribution capabilities, density curves, and QQ-plots. These visualizations assist detect potential variations in form, location, or dispersion between two distributions.
Such graphical analyses present a vital first step: they information the investigation and assist formulate hypotheses. Nonetheless, they have to be complemented by statistical assessments to verify observations and attain rigorous conclusions. These assessments embody:
- Parametric assessments, comparable to Scholar’s t-test (comparability of means),
- Nonparametric assessments, such because the Kolmogorov–Smirnov check (comparability of distributions), the chi-squared check (for categorical variables), and Welch’s check (for unequal variances).
These approaches are properly offered within the article by @matteo-courthoud. Past them, two indicators are notably related in credit score danger evaluation for assessing distributional drift between populations and supporting decision-making: the Inhabitants Stability Index (PSI) and Cramér’s V
2.1. The Inhabitants Stability Index (PSI)
The PSI is a elementary device within the credit score trade. It measures the distinction between two distributions of the identical variable:
- for instance, between the coaching dataset and a newer software dataset,
- or between a reference dataset at time T0 and one other at time T1.
In different phrases, the PSI quantifies how a lot a inhabitants has drifted over time or throughout totally different scopes.
Right here’s the way it works in apply:
- For a categorical variable, we compute the proportion of observations in every class for each datasets.
- For a steady variable, we first discretize it into bins. In apply, deciles are sometimes used to acquire a balanced distribution.
The PSI then compares, bin by bin, the proportions noticed within the reference dataset versus the goal dataset. The ultimate indicator aggregates these variations utilizing a logarithmic system:
Right here, pᵢ and qᵢ symbolize the proportions in bin i for the reference dataset and the goal dataset, respectively. The PSI will be computed simply in an Excel file:

The interpretation is very intuitive:
- A smaller PSI means the 2 distributions are nearer.
- A PSI of 0 means the distributions are an identical.
- A really giant PSI (tending towards infinity) means the 2 distributions are essentially totally different.
In apply, trade tips typically use the next thresholds:
- PSI < 0.1: the inhabitants is secure,
- 0.1 ≤ PSI < 0.25: the shift is noticeable—monitor carefully,
- PSI ≥ 0.25: the shift is critical—the mannequin could not be dependable.
2.2. Cramér’s V
When assessing the representativeness of a categorical variable (or a discretized continuous variable) between two datasets, a natural starting point is the Chi-square test of independence.
We build a contingency table crossing:
- the categories (modalities) of the variable of interest, and
- an indicator variable for dataset membership (Dataset 1 / Dataset 2).
The test is based on the following statistic:

where Oij are the observed counts and Eij are the expected counts under the assumption of independence.
- Null hypothesis H0: the variable has the same distribution in both datasets (independence).
- Alternative hypothesis H1 : the distributions differ.
If H0 is rejected, we conclude that the variable does not follow the same distribution across the two datasets.
However, the Chi-square test has a major limitation: it only provides a binary answer (reject / do not reject), and its power is highly sensitive to sample size. With very large datasets, even tiny differences can appear statistically significant.
To address this limitation, we use Cramér’s V, which rescales the Chi-square statistic to produce a normalized measure of association bounded between 0 and 1:

where n is the total sample size, r is the number of rows, and c is the number of columns in the contingency table.
The interpretation is intuitive:
- V≈0 ⇒ The distributions are very similar; representativeness is strong.
- V→1 ⇒ The difference between distributions is large; the datasets are structurally different.
Unlike the Chi-square test, which simply answers “yes” or “no,” Cramér’s V provides a graded measure of the strength of the difference. This allows us to assess whether the difference is negligible, moderate, or substantial.
We use the same thresholds as those applied for the PSI to draw our conclusions. For the PSI and Cramér’s V indicators, if the distribution of one or more variables differs significantly between the two datasets, we conclude that they are not representative.
3. Measuring Representativeness with PSI and Cramér’s V in Python.
In a previous article, we utilized totally different variable choice strategies to scale back the Communities & Crime dataset to only 16 explanatory variables. This step was important to simplify the mannequin whereas holding essentially the most related data.
This dataset additionally features a variable referred to as fold, which splits the information into 10 subsamples. These folds are generally utilized in cross-validation: they permit us to check the robustness of a mannequin by coaching it on one a part of the information and validating it on one other. For cross-validation to be dependable, every fold needs to be consultant of the worldwide dataset:
- To make sure legitimate efficiency estimates.
- To stop bias: a non-representative fold can distort mannequin outcomes
- To help generalization: consultant folds present a greater indication of how the mannequin will carry out on new information.
On this instance, we are going to deal with checking whether or not fold 1 is consultant of the worldwide dataset utilizing our two indicators: PSI and Cramer’s V by evaluating the distribution of 16 variables throughout the 2 samples. We’ll proceed in two steps:
Step 1: Begin with the Goal Variable
We begin with the target variable. The idea is simple: compare its distribution between fold 1 and the entire dataset. To quantify this difference, we’ll use two complementary indicators:
- the Population Stability Index (PSI), which measures distributional shifts,
- Cramér’s V, which measures the strength of association between two categorical variables.
Step 2: Automating the Analysis for All Variables
After illustrating the approach with the target, we extend it to all features. We’ll build a Python function that computes PSI and Cramér’s V for each of the 16 explanatory variables, as well as for the target variable.
To make the results easy to interpret, we’ll export everything into an Excel file with:
- one sheet per variable, showing the detailed comparison by segment,
- a Summary tab, aggregating results across all variables.
3.1 Comparing the target variable ViolentCrimesPerPop between the global dataset (reference) and fold 1 (target)
Before applying statistical tests or building decision indicators, it is essential to conduct a descriptive and graphical analysis. There are not just formalities; they provide an early intuition about the differences between populations and help interpreting the results. In practice, a well-chosen chart often reveals the conclusions that indicators like PSI or Cramér’s V will later confirm (or challenge).
For visualization, we proceed in three steps:
1. Comparing continuous distributions We begin with graphical tools such as boxplots, cumulative distribution functions, and probability density plots. These visualizations provide an intuitive way to examine differences in the target variable’s distribution between the two datasets.
2. Discretization into quantiles Next, we discretize the variable in the reference dataset using quartiles (Q1, Q2, Q3, Q4), which creates five classes (Q1 through Q5). We then apply the exact same cut-off points to the target dataset, ensuring that each observation is mapped to intervals defined from the reference. This guarantees comparability between the two distributions.
3. Comparing categorical distributions Finally, once the variable has been discretized, we can use visualization methods suited for categorical data — such as bar charts — to compare how frequencies are distributed across the two datasets.
The process depends on the type of variable:
For a continuous variable:
- Start with standard visualizations (boxplots, cumulative distributions, and density plots).
- Next, split the variable into segments (Q1 to Q5) based on the reference dataset’s quantiles.
- Finally, treat these segments as categories and compare their distributions.
For a categorical variable:
- No discretization is needed — it’s already in categorical form.
- Go straight to comparing category distributions, for example with a bar chart.
The code below prepares the two datasets we want to compare and then visualizes the target variable with a boxplot, showing its distribution in both the global dataset and in fold 1.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import chi2_contingency, ks_2samp
data = pd.read_csv("communities_data.csv")
# filter sur fold =1
data_ref = data
data_target = data[data["fold"] == 1]
# compare the two distribution of "ViolentCrimesPerPop" in the reference and target datasets with boxplots
# Build datasets with a "Group" column
df_ref = pd.DataFrame({
"ViolentCrimesPerPop": data_ref["ViolentCrimesPerPop"],
"Group": "Reference"
})
df_target = pd.DataFrame({
"ViolentCrimesPerPop": data_target["ViolentCrimesPerPop"],
"Group": "Target"
})
# Merge them
df_all = pd.concat([df_ref, df_target])
plt.figure(figsize=(8, 6))
# Boxplot with both distributions overlayed
sns.boxplot(
x="Group",
y="ViolentCrimesPerPop",
data=df_all,
palette="Set2",
width=0.6,
fliersize=3
)
# Add mean points
means = df_all.groupby("Group")["ViolentCrimesPerPop"].mean()
for i, m in enumerate(means):
plt.scatter(i, m, color="red", marker="D", s=50, zorder=3, label="Mean" if i == 0 else "")
# Title tells the story
plt.title("Violent Crimes Per Population by Group", fontsize=14, weight="bold")
plt.suptitle("Both groups show nearly identical distributions",
fontsize=10, color="gray")
plt.ylabel("Violent Crimes (Per Pop)", fontsize=12)
plt.xlabel("")
# Cleaner look
sns.despine()
plt.grid(axis="y", linestyle="--", alpha=0.5, visible=False)
plt.legend()
plt.show()
print(len(data.columns))
The figure above suggests that both groups share similar distributions for the ViolentCrimesPerPop variable. To take a closer look, we can use Kernel Density Estimation (KDE) plots, which provide a smooth view of the underlying distribution and make it easier to spot subtle differences.
plt.figure(figsize=(8, 6))
# KDE plots with better styling
sns.kdeplot(
data=df_all,
x="ViolentCrimesPerPop",
hue="Group",
fill=True, # use shading for overlap
alpha=0.4, # transparency to show overlap
common_norm=False,
palette="Set2",
linewidth=2
)
# KS-test for distribution difference
g1 = df_all[df_all["Group"] == df_all["Group"].unique()[0]]["ViolentCrimesPerPop"]
g2 = df_all[df_all["Group"] == df_all["Group"].unique()[1]]["ViolentCrimesPerPop"]
stat, pval = ks_2samp(g1, g2)
# Add annotation
plt.text(df_all["ViolentCrimesPerPop"].mean(),
plt.ylim()[1]*0.9,
f"KS-test p-value = {pval:.3f}nNo significant difference observed",
ha="center", fontsize=10, color="black")
# Titles with story
plt.title("Kernel Density Estimation of Violent Crimes Per Population", fontsize=14, weight="bold")
plt.suptitle("Distributions overlap almost completely between groups", fontsize=10, color="gray")
plt.xlabel("Violent Crimes (Per Pop)")
plt.ylabel("Density")
sns.despine()
plt.grid(False)
plt.show()
The KDE graph confirms that the two distributions are very similar, showing a high degree of overlap. The Kolmogorov-Smirnov (KS) statistical test of 0.976 also indicates that there is no significant difference between the two groups. To extend the analysis, we can now examine the cumulative distribution of the target variable.
# Cumulative distribution
plt.figure(figsize=(9, 6))
sns.histplot(
data=df_all,
x="ViolentCrimesPerPop",
hue="Group",
stat="density",
common_norm=False,
fill=False,
element="step",
bins=len(df_all),
cumulative=True,
)
# Titles tell the story
plt.title("Cumulative Distribution of Violent Crimes Per Population", fontsize=14, weight="bold")
plt.suptitle("ECDFs overlap extensively; central tendencies are nearly identical", fontsize=10)
# Labels & cleanup
plt.xlabel("Violent Crimes (Per Pop)")
plt.ylabel("Cumulative proportion")
plt.grid(visible=False)
plt.show()
The cumulative distribution plot provides additional evidence that the two groups are very similar. The curves overlap almost completely, suggesting that their distributions are nearly identical in both central tendency and spread.
As a next step, we’ll discretize the variable into quantiles in the reference dataset and then apply the same cut-off points to the target dataset (fold 1). The code below demonstrates how to do this. Finally, we’ll compare the resulting distributions using a bar chart.
def bin_numeric(ref, tgt, n_bins=5):
"""
Discretize a numeric variable into quantile bins (ex: quintiles).
- Quantile thresholds are computed only on the reference dataset.
- Extend bins with -inf and +inf to cover all possible values.
- Returns:
* ref binned
* tgt binned
* bin labels (Q1, Q2, ...)
"""
edges = np.unique(ref.dropna().quantile(np.linspace(0, 1, n_bins + 1)).values)
if len(edges) < 3: # if variable is almost constant
edges = np.array([-np.inf, np.inf])
else:
edges[0], edges[-1] = -np.inf, np.inf
labels = [f"Q{i}" for i in range(1, len(edges))]
return (
pd.cut(ref, bins=edges, labels=labels, include_lowest=True),
pd.cut(tgt, bins=edges, labels=labels, include_lowest=True),
labels
)
# Apply binning
ref_binned, tgt_binned, bin_labels = bin_numeric(data_ref["ViolentCrimesPerPop"], data_target["ViolentCrimesPerPop"], n_bins=5)
# Effectifs par segment pour Reference et Target
ref_counts = ref_binned.value_counts().reindex(bin_labels, fill_value=0)
tgt_counts = tgt_binned.value_counts().reindex(bin_labels, fill_value=0)
# Convertir en proportions
ref_props = ref_counts / ref_counts.sum()
tgt_props = tgt_counts / tgt_counts.sum()
# Construire un DataFrame pour seaborn
df_props = pd.DataFrame({
"Segment": bin_labels,
"Reference": ref_props.values,
"Target": tgt_props.values
})
# Restructurer en format long
df_long = df_props.melt(id_vars="Segment",
value_vars=["Reference", "Target"],
var_name="Source",
value_name="Proportion")
# Style sobre
sns.set_theme(style="whitegrid")
# Barplot avec proportions
plt.figure(figsize=(8,6))
sns.barplot(
x="Segment", y="Proportion", hue="Source",
data=df_long, palette=["#4C72B0", "#55A868"] # bleu & vert sobres
)
# Titre et légende
# Titles with story
plt.title("Proportion Comparison by Segment (ViolentCrimesPerPop)", fontsize=14, weight="bold")
plt.suptitle("Across all quantile segments (Q1–Q5), proportions are nearly identical", fontsize=10, color="gray")
plt.xlabel("Quantile Segment (Q1 - Q5)")
plt.ylabel("Proportion")
plt.legend(title="Dataset", loc="upper right")
plt.grid(False)
plt.show()
As before, we reach the same conclusion: the distributions in the reference and target datasets are very similar. To move beyond visual inspection, we will now compute the Population Stability Index (PSI) and Cramér’s V statistic. These metrics allow us to quantify the differences between distributions; both for all variables in general and for the target variable ViolentCrimesPerPop in particular.
3.2 Automating the Analysis for All Variables
As mentioned earlier, the results of the distribution comparisons for each variable between the two datasets, calculated using PSI and Cramér’s V, are presented in separate sheets within a single Excel file.
To illustrate, we begin by examining the results for the target variable ViolentCrimesPerPop when comparing the global dataset (reference) with fold 1 (target). The table 1 below summarizes how both PSI and Cramér’s V are computed.

Since both PSI and Cramér’s V are below 0.1, we can conclude that the target variable ViolentCrimesPerPop follows the same distribution in both datasets.
The code that generated this table is shown below. The same code can also be used to produce results for all variables and export them into an Excel file called representativity.xlsx.
EPS = 1e-12 # A very small constant to avoid division by zero or log(0)
# ============================================================
# 1. Basic functions
# ============================================================
def safe_proportions(counts):
"""
Convert raw counts into proportions in a safe way.
- If the total count = 0, return all zeros (to avoid division by zero).
- Clip values so no proportion is exactly 0 or 1 (numerical stability).
"""
total = counts.sum()
if total == 0:
return np.zeros_like(counts, dtype=float)
p = counts / total
return np.clip(p, EPS, 1.0)
def calculate_psi(p_ref, p_tgt):
"""
Compute the Population Stability Index (PSI) between two distributions.
PSI = sum( (p_ref - p_tgt) * log(p_ref / p_tgt) )
Interpretation:
- PSI < 0.1 → stable
- 0.1–0.25 → moderate shift
- > 0.25 → major shift
"""
p_ref = np.clip(p_ref, EPS, 1.0)
p_tgt = np.clip(p_tgt, EPS, 1.0)
return float(np.sum((p_ref - p_tgt) * np.log(p_ref / p_tgt)))
def calculate_cramers_v(contingency):
"""
Compute Cramér's V statistic for association between two categorical variables.
- Input: a 2 x K contingency table (counts).
- Uses Chi² test.
- Normalizes the result to [0, 1].
* 0 → no association
* 1 → perfect association
"""
chi2, _, _, _ = chi2_contingency(contingency, correction=False)
n = contingency.sum()
r, c = contingency.shape
if n == 0 or min(r - 1, c - 1) == 0:
return 0.0
return np.sqrt(chi2 / (n * (min(r - 1, c - 1))))
# ============================================================
# 2. Preparing variables
# ============================================================
def bin_numeric(ref, tgt, n_bins=5):
"""
Discretize a numeric variable into quantile bins (ex: quintiles).
- Quantile thresholds are computed only on the reference dataset.
- Extend bins with -inf and +inf to cover all possible values.
- Returns:
* ref binned
* tgt binned
* bin labels (Q1, Q2, ...)
"""
edges = np.unique(ref.dropna().quantile(np.linspace(0, 1, n_bins + 1)).values)
if len(edges) < 3: # if variable is almost constant
edges = np.array([-np.inf, np.inf])
else:
edges[0], edges[-1] = -np.inf, np.inf
labels = [f"Q{i}" for i in range(1, len(edges))]
return (
pd.cut(ref, bins=edges, labels=labels, include_lowest=True),
pd.cut(tgt, bins=edges, labels=labels, include_lowest=True),
labels
)
def prepare_counts(ref, tgt, n_bins=5):
"""
Prepare frequency counts for one variable.
- If numeric: discretize into quantile bins.
- If categorical: take all categories present in either dataset.
Returns:
segments, counts in reference, counts in target
"""
if pd.api.types.is_numeric_dtype(ref) and pd.api.types.is_numeric_dtype(tgt):
ref_b, tgt_b, labels = bin_numeric(ref, tgt, n_bins)
segments = labels
else:
segments = sorted(set(ref.dropna().unique()) | set(tgt.dropna().unique()))
ref_b, tgt_b = ref.astype(str), tgt.astype(str)
ref_counts = ref_b.value_counts().reindex(segments, fill_value=0)
tgt_counts = tgt_b.value_counts().reindex(segments, fill_value=0)
return segments, ref_counts, tgt_counts
# ============================================================
# 3. Analysis per variable
# ============================================================
def analyze_variable(ref, tgt, n_bins=5):
"""
Analyze a single variable between two datasets.
Steps:
- Build counts by segment (bin for numeric, category for categorical).
- Compute PSI by segment and Global PSI.
- Compute Cramér's V from the contingency table.
- Return:
DataFrame with details
Summary dictionary (psi, v_cramer)
"""
segments, ref_counts, tgt_counts = prepare_counts(ref, tgt, n_bins)
p_ref, p_tgt = safe_proportions(ref_counts.values), safe_proportions(tgt_counts.values)
# PSI
psi_global = calculate_psi(p_ref, p_tgt)
psi_by_segment = (p_ref - p_tgt) * np.log(p_ref / p_tgt)
# Cramér's V
contingency = np.vstack([ref_counts.values, tgt_counts.values])
v_cramer = calculate_cramers_v(contingency)
# Build detailed results table
df = pd.DataFrame({
"Segment": segments,
"Count Reference": ref_counts.values,
"Count Target": tgt_counts.values,
"Percent Reference": p_ref,
"Percent Target": p_tgt,
"PSI by Segment": psi_by_segment
})
# Add summary lines at the bottom of the table
df.loc[len(df)] = ["Global PSI", np.nan, np.nan, np.nan, np.nan, psi_global]
df.loc[len(df)] = ["Cramer's V", np.nan, np.nan, np.nan, np.nan, v_cramer]
return df, {"psi": psi_global, "v_cramer": v_cramer}
# ============================================================
# 4. Excel reporting utilities
# ============================================================
def apply_traffic_light(ws, wb, first_row, last_row, col, low, high):
"""
Apply conditional formatting (traffic light colors) to a numeric column in Excel:
- green if value < low
- orange if low <= value <= high
- red if value > high
Note: first_row, last_row, and col are zero-based indices (xlsxwriter convention).
"""
green = wb.add_format({"bg_color": "#C6EFCE", "font_color": "#006100"})
orange = wb.add_format({"bg_color": "#FCD5B4", "font_color": "#974706"})
red = wb.add_format({"bg_color": "#FFC7CE", "font_color": "#9C0006"})
if last_row < first_row:
return # nothing to color
ws.conditional_format(first_row, col, last_row, col,
{"type": "cell", "criteria": "<", "value": low, "format": green})
ws.conditional_format(first_row, col, last_row, col,
{"type": "cell", "criteria": "between", "minimum": low, "maximum": high, "format": orange})
ws.conditional_format(first_row, col, last_row, col,
{"type": "cell", "criteria": ">", "value": high, "format": red})
def representativity_report(ref_df, tgt_df, variables, output="representativity.xlsx",
n_bins=5, psi_thresholds=(0.10, 0.25),
v_thresholds=(0.10, 0.25), color_summary=True):
"""
Build a representativity report across multiple variables and export to Excel.
For each variable:
- Create a sheet with detailed PSI by segment, Global PSI, and Cramer's V.
- Apply traffic light colors for easier interpretation.
Create one "Résumé" sheet with overall Global PSI and Cramer's V for all variables.
"""
summary = []
with pd.ExcelWriter(output, engine="xlsxwriter") as writer:
wb = writer.book
fmt_header = wb.add_format({"bold": True, "bg_color": "#0070C0",
"font_color": "white", "align": "center"})
fmt_pct = wb.add_format({"num_format": "0.00%"})
fmt_ratio = wb.add_format({"num_format": "0.000"})
fmt_int = wb.add_format({"num_format": "0"})
for var in variables:
# Analyze variable
df, meta = analyze_variable(ref_df[var], tgt_df[var], n_bins)
sheet = var[:31] # Excel sheet names are limited to 31 characters
df.to_excel(writer, sheet_name=sheet, index=False)
ws = writer.sheets[sheet]
# Format headers and columns
for j, col in enumerate(df.columns):
ws.write(0, j, col, fmt_header)
ws.set_column(0, 0, 18)
ws.set_column(1, 2, 16, fmt_int)
ws.set_column(3, 4, 20, fmt_pct)
ws.set_column(5, 5, 18, fmt_ratio)
nrows = len(df) # number of data rows (excluding header)
col_psi = 5 # "PSI by Segment" column index
# PSI by Segment rows
apply_traffic_light(ws, wb, first_row=1, last_row=max(1, nrows-2),
col=col_psi, low=psi_thresholds[0], high=psi_thresholds[1])
# Global PSI row (second to last)
apply_traffic_light(ws, wb, first_row=nrows-1, last_row=nrows-1,
col=col_psi, low=psi_thresholds[0], high=psi_thresholds[1])
# Cramer's V row (last row)
apply_traffic_light(ws, wb, first_row=nrows, last_row=nrows,
col=col_psi, low=v_thresholds[0], high=v_thresholds[1])
# Add summary info for Résumé sheet
summary.append({"Variable": var,
"Global PSI": meta["psi"],
"Cramer's V": meta["v_cramer"]})
# Résumé sheet
df_sum = pd.DataFrame(summary)
df_sum.to_excel(writer, sheet_name="Résumé", index=False)
ws = writer.sheets["Résumé"]
for j, col in enumerate(df_sum.columns):
ws.write(0, j, col, fmt_header)
ws.set_column(0, 0, 28)
ws.set_column(1, 2, 16, fmt_ratio)
# Apply traffic light to summary sheet
if color_summary and len(df_sum) > 0:
last = len(df_sum)
# PSI column
apply_traffic_light(ws, wb, 1, last, 1, psi_thresholds[0], psi_thresholds[1])
# Cramer's V column
apply_traffic_light(ws, wb, 1, last, 2, v_thresholds[0], v_thresholds[1])
return output
# ============================================================
# Example
# ============================================================
if __name__ == "__main__":
# columns namees privées de fold
columns = [x for x in data.columns if x != "fold"]
# Generate the report
path = representativity_report(data_ref, data_target, columns, output="representativity.xlsx")
print(f" Report generated: {path}")inally, Table 2 shows the last sheet of the file, titled Summary, which brings together the results for all variables of interest.

This synthesis provides an overall view of representativeness between the two datasets, making interpretation and decision-making much easier. Since both PSI and Cramér’s V are below 0.1, we can conclude that all variables follow the same distribution in the global dataset and in fold 1. Therefore, fold 1 can be considered representative of the global dataset.
Conclusion
In this post, we explored how to study representativeness between two datasets by comparing the distributions of their variables. We introduced two key indicators Population stability index(PSI) and Cramér’s V, that are both easy to use, easy to interpret, and highly valuable for decision-making.
We also showed how these analyses can be automated, with results saved directly into an Excel file.
The main takeaway is this: if you build a model and end up with overfitting, one possible reason may be that your training and test sets are not representative of each other. A simple way to prevent this is to always run a representativity analysis between datasets. Variables that show representativity issues can then guide you in stratifying your data when splitting it into training and test sets. What about you? In what situations do you study representativeness between two data sets, for what reasons, and using what methods?
References
Yurdakul, B. (2018). Statistical properties of population stability index. Western Michigan University.
Redmond, M. (2002). Communities and Crime [Dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C53W3X.
Data & Licensing
The dataset used in this article is licensed under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.
This license allows anyone to share and adapt the dataset for any purpose, including commercial use, provided that proper attribution is given to the source.
For more details, see the official license text: CC BY 4.0.
Disclaimer
I write to be taught so errors are the norm, despite the fact that I strive my greatest. Please, if you spot them, let me know. I additionally respect recommendations on new subjects!