is a statistical method used to reply the query: “How lengthy will one thing final?” That “one thing” might vary from a affected person’s lifespan to the sturdiness of a machine part or the period of a consumer’s subscription.
One of the crucial broadly used instruments on this space is the Kaplan-Meier estimator.
Born on this planet of biology, Kaplan-Meier made its debut monitoring life and dying. However like several true celeb algorithm, it didn’t keep in its lane. As of late, it’s exhibiting up in enterprise dashboards, advertising and marketing groups, and churn analyses all over the place.
However right here’s the catch: enterprise isn’t biology. It’s messy, unpredictable, and stuffed with plot twists. Because of this there are a few points that make our lives harder after we attempt to use survival evaluation within the enterprise world.
To start with, we’re sometimes not simply fascinated by whether or not a buyer has “survived” (no matter survival might imply on this context), however reasonably in how a lot of that particular person’s financial worth has survived.
Secondly, opposite to biology, it’s very potential for patrons to “die” and “resuscitate” a number of instances (consider once you unsubscribe/resubscribe to an internet service).
On this article, we are going to see easy methods to prolong the classical Kaplan-Meier method in order that it higher fits our wants: modeling a steady (financial) worth as a substitute of a binary one (life/dying) and permitting “resurrections”.
A refresher on the Kaplan-Meier estimator
Let’s pause and rewind for a second. Earlier than we begin customizing Kaplan-Meier to suit our enterprise wants, we want a fast refresher on how the traditional model works.
Suppose you had 3 topics (let’s say lab mice) and also you gave them a drugs you want to check. The medication was given at totally different moments in time: topic a obtained it in January, topic b in April, and topic c in Could.
Then, you measure how lengthy they survive. Topic a died after 6 months, topic c after 4 months, and topic b remains to be alive on the time of the evaluation (November).
Graphically, we will signify the three topics as follows:
Now, even when we needed to measure a easy metric, like common survival, we’d face an issue. In truth, we don’t know the way lengthy topic b will survive, as it’s nonetheless alive immediately.
This can be a classical drawback in statistics, and it’s known as “proper censoring“.
Proper censoring is stats-speak for “we don’t know what occurred after a sure level” and it’s a giant deal in survival evaluation. So large that it led to the event of one of the crucial iconic estimators in statistical historical past: the Kaplan-Meier estimator, named after the duo who launched it again within the Fifties.
So, how does Kaplan-Meier deal with our drawback?
First, we align the clocks. Even when our mice have been handled at totally different instances, what issues is time since remedy. So we reset the x-axis to zero for everybody — day zero is the day they obtained the drug.

Now that we’re all on the identical timeline, we wish to construct one thing helpful: an mixture survival curve. This curve tells us the chance {that a} typical mouse in our group will survive at the least x months post-treatment.
Let’s comply with the logic collectively.
- As much as time 3? Everybody’s nonetheless alive. So survival = 100%. Simple.
- At time 4, mouse c dies. Because of this out of the three mice, solely 2 of them survived after time 4. That offers us a survival charge of 67% at time 4.
- Then at time 6, mouse a checks out. Of the two mice that had made it to time 6, only one survived, so the survival charge from time 5 to six is 50%. Multiply that by the earlier 67%, and we get 33% survival as much as time 6.
- After time 7 we don’t produce other topics which might be noticed alive, so the curve has to cease right here.
Let’s plot these outcomes:

Since code is commonly simpler to grasp than phrases, let’s translate this to Python. Now we have the next variables:
kaplan_meier, an array containing the Kaplan-Meier estimates for every cut-off date, e.g. the chance of survival as much as time t.obs_t, an array that tells us whether or not a person is noticed (e.g., not right-censored) at time t.surv_t, boolean array that tells us whether or not every particular person is alive at time t.surv_t_minus_1, boolean array that tells us whether or not every particular person is alive at time t-1.
All we’ve got to do is to take all of the people noticed at t, compute their survival charge from t-1 to t (survival_rate_t), and multiply it by the survival charge as much as time t-1 (km[t-1]) to acquire the survival charge as much as time t (km[t]). In different phrases,
survival_rate_t = surv_t[obs_t].sum() / surv_t_minus_1[obs_t].sum()
kaplan_meier[t] = kaplan_meier[t-1] * survival_rate_tthe place, after all, the start line is kaplan_meier[0] = 1.
For those who don’t wish to code this from scratch, the Kaplan-Meier algorithm is on the market within the Python library lifelines, and it may be used as follows:
from lifelines import KaplanMeierFitter
KaplanMeierFitter().match(
durations=[6,7,4],
event_observed=[1,0,1],
).survival_function_["KM_estimate"]For those who use this code, you’ll receive the identical outcome we’ve got obtained manually with the earlier snippet.
To this point, we’ve been hanging out within the land of mice, medication, and mortality. Not precisely your common quarterly KPI assessment, proper? So, how is this handy in enterprise?
Transferring to a enterprise setting
To this point, we’ve handled “dying” as if it’s apparent. In Kaplan-Meier land, somebody both lives or dies, and we will simply log the time of dying. However now let’s stir in some real-world enterprise messiness.
What even is “dying” in a enterprise context?
It seems it’s not simple to reply this query, at the least for a few causes:
- “Dying” will not be simple to outline. Let’s say you’re working at an e-commerce firm. You wish to know when a consumer has “died”. Do you have to depend them as lifeless after they delete their account? That’s simple to trace… however too uncommon to be helpful. What if they only begin buying much less? However how a lot much less is lifeless? Per week of silence? A month? Two? You see the issue. The definition of “dying” is unfair, and relying on the place you draw the road, your evaluation may inform wildly totally different tales.
- “Dying” will not be everlasting. Kaplan-Meier has been conceived for organic functions by which as soon as a person is lifeless there isn’t any return. However in enterprise functions, resurrection will not be solely potential however fairly frequent. Think about a streaming service for which individuals pay a month-to-month subscription. It’s simple to outline “dying” on this case: it’s when customers cancel their subscriptions. Nonetheless, it’s fairly frequent that, a while after cancelling, they re-subscribe.
So how does all this play out in information?
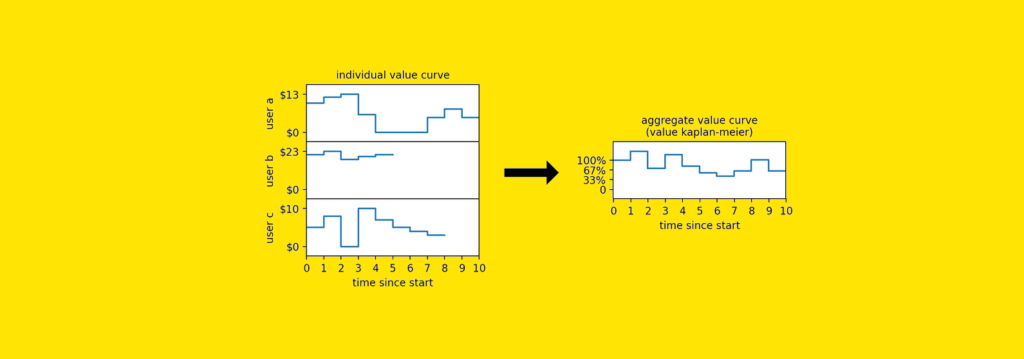
Let’s stroll by way of a toy instance. Say we’ve got a consumer on our e-commerce platform. Over the previous 10 months, right here’s how a lot they’ve spent:

To squeeze this into the Kaplan-Meier framework, we have to translate that spending habits right into a life-or-death choice.
So we make a rule: if a consumer stops spending for two consecutive months, we declare them “inactive”.
Graphically, this rule appears like the next:

Because the consumer spent $0 for 2 months in a row (month 4 and 5) we are going to think about this consumer inactive ranging from month 4 on. And we are going to try this regardless of the consumer began spending once more in month 7. It is because, in Kaplan-Meier, resurrections are assumed to be not possible.
Now let’s add two extra customers to our instance. Since we’ve got determined a rule to show their worth curve right into a survival curve, we will additionally compute the Kaplan-Meier survival curve:

By now, you’ve most likely observed how a lot nuance (and information) we’ve thrown away simply to make this work. Consumer a got here again from the lifeless — however we ignored that. Consumer c‘s spending dropped considerably — however Kaplan-Meier doesn’t care, as a result of all it sees is 1s and 0s. We pressured a steady worth (spending) right into a binary field (alive/lifeless), and alongside the best way, we misplaced a complete lot of knowledge.
So the query is: can we prolong Kaplan-Meier in a manner that:
- retains the unique, steady information intact,
- avoids arbitrary binary cutoffs,
- permits for resurrections?
Sure, we will. Within the subsequent part, I’ll present you the way.
Introducing “Worth Kaplan-Meier”
Let’s begin with the straightforward Kaplan-Meier system we’ve got seen earlier than.
# kaplan_meier: array containing the Kaplan-Meier estimates,
# e.g. the chance of survival as much as time t
# obs_t: array, whether or not a topic has been noticed at time t
# surv_t: array, whether or not a topic was alive at time t
# surv_t_minus_1: array, whether or not a topic was alive at time t−1
survival_rate_t = surv_t[obs_t].sum() / surv_t_minus_1[obs_t].sum()
kaplan_meier[t] = kaplan_meier[t-1] * survival_rate_tThe primary change we have to make is to switch surv_t and surv_t_minus_1, that are boolean arrays that inform us whether or not a topic is alive (1) or lifeless (0) with arrays that inform us the (financial) worth of every topic at a given time. For this function, we will use two arrays named val_t and val_t_minus_1.
However this isn’t sufficient, as a result of since we’re coping with steady worth, each consumer is on a special scale and so, assuming that we wish to weigh them equally, we have to rescale them primarily based on some particular person worth. However what worth ought to we use? Probably the most affordable alternative is to make use of their preliminary worth at time 0, earlier than they have been influenced by no matter remedy we’re making use of to them.
So we additionally want to make use of one other vector, named val_t_0 that represents the worth of the person at time 0.
# value_kaplan_meier: array containing the Worth Kaplan-Meier estimates
# obs_t: array, whether or not a topic has been noticed at time t
# val_t_0: array, consumer worth at time 0
# val_t: array, consumer worth at time t
# val_t_minus_1: array, consumer worth at time t−1
value_rate_t = (
(val_t[obs_t] / val_t_0[obs_t]).sum()
/ (val_t_minus_1[obs_t] / val_t_0[obs_t]).sum()
)
value_kaplan_meier[t] = value_kaplan_meier[t-1] * value_rate_tWhat we’ve constructed is a direct generalization of Kaplan-Meier. In truth, if you happen to set val_t = surv_t, val_t_minus_1 = surv_t_minus_1, and val_t_0 as an array of 1s, this system collapses neatly again to our authentic survival estimator. So sure—it’s legit.
And right here is the curve that we’d receive when utilized to those 3 customers.

Let’s name this new model the Worth Kaplan-Meier estimator. In truth, it solutions the query:
How a lot % of worth remains to be surviving, on common, after x time?
We’ve obtained the idea. However does it work within the wild?
Utilizing Worth Kaplan-Meier in follow
For those who take the Worth Kaplan-Meier estimator for a spin on real-world information and evaluate it to the nice outdated Kaplan-Meier curve, you’ll possible discover one thing comforting — they usually have the identical form. That’s a very good signal. It means we haven’t damaged something basic whereas upgrading from binary to steady.
However right here’s the place issues get fascinating: Worth Kaplan-Meier often sits a bit above its conventional cousin. Why? As a result of on this new world, customers are allowed to “resurrect”. Kaplan-Meier, being the extra inflexible of the 2, would’ve written them off the second they went quiet.
So how will we put this to make use of?
Think about you’re working an experiment. At time zero, you begin a brand new remedy on a gaggle of customers. No matter it’s, you’ll be able to observe how a lot worth “survives” in each the remedy and management teams over time.
And that is what your output will most likely appear to be:

Conclusion
Kaplan-Meier is a broadly used and intuitive technique for estimating survival capabilities, particularly when the result is a binary occasion like dying or failure. Nonetheless, many real-world enterprise eventualities contain extra complexity — resurrections are potential, and outcomes are higher represented by steady values reasonably than a binary state.
In such circumstances, Worth Kaplan-Meier presents a pure extension. By incorporating the financial worth of people over time, it permits a extra nuanced understanding of worth retention and decay. This technique preserves the simplicity and interpretability of the unique Kaplan-Meier estimator whereas adapting it to higher mirror the dynamics of buyer habits.
Worth Kaplan-Meier tends to offer the next estimate of retained worth in comparison with Kaplan-Meier, as a result of its capacity to account for recoveries. This makes it notably helpful in evaluating experiments or monitoring buyer worth over time.